内容提供者
勾股定理的应用-最短距离.ppt
2024-06-18
10金币
198KB
15页
sy****28
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共15页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
勾股定理的应用-最短距离.ppt
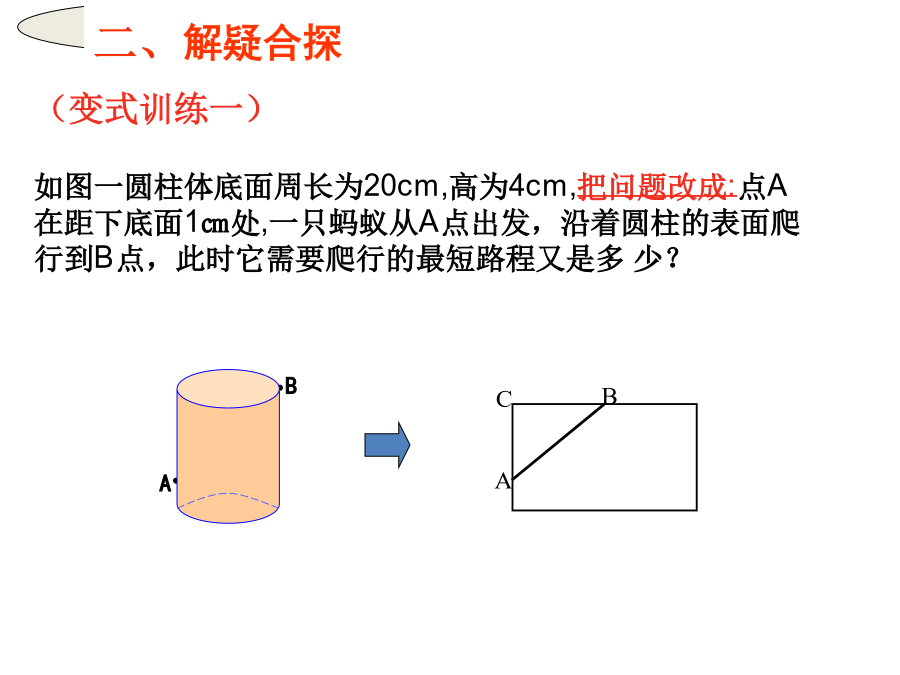
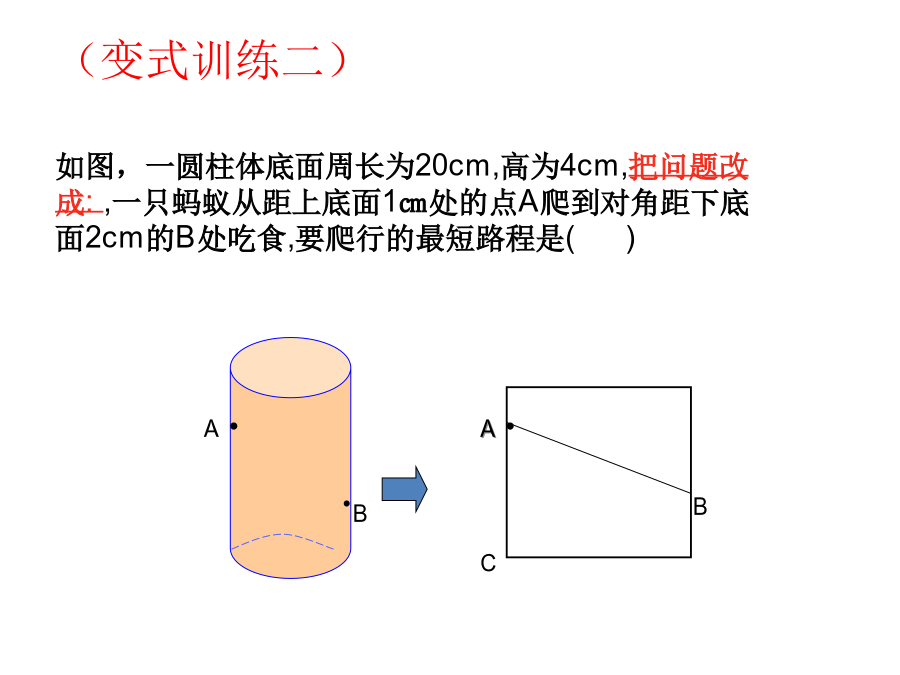
学习目标：复习回顾1、前面我们已经学习了勾股定理，你能说出勾股定理的内容吗？它的表达式是什么？勾股定理的内容:。2.若直角三角形的两条直角边的长分别为a、b,斜边c,则满足。3.平面内两点之间最短。创设情境，导入新课自学提示思路小结：请你自编一道类似的题目，与同学们分享三、质疑再探如图：圆柱形玻璃杯,高为12cm,底面圆的周长为18cm,在杯子内壁离杯底4cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯子外壁，距离杯子上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为多少?本节你学会了什么数学思想?学会
2024-06-18
10
198KB
勾股定理的应用最短距离.pptx
会计学思路小结：牛刀小试例2.一个三级台阶，它的每一级的长、宽和高分别等于5cm，3cm和1cm，A和B是这个台阶的两个相对的端点，A点上有一只蚂蚁，想到B点去吃可口的食物.请你想一想，这只蚂蚁从A点出发，沿着台阶面爬到B点，最短线路是多少？想一想例3.如果盒子换成长为4cm，宽为2cm，高为1cm的长方体盒子，蚂蚁沿着表面从A点爬行到B点的最短路程又是多少呢？分析：蚂蚁由A爬到B过程中较短的路线有多少种情况？蚂蚁沿着长方体表面从注爬到B的最短距离的平方分别是：例4.如图，一个的长方体盒子的长、宽、高分别
2024-09-15
20
556KB
勾股定理的应用（最短距离） (2).pptx
勾股定理的应用(最短距离）教学目标：知识与技能1.能运用勾股定理的数学模型解决现实世界的实际问题。2.通过例题的分析和解决，让学生感受勾股定理在实际生活中的应用。情感、态度与价值观教学重点：一、复习引入：探究一：如下图，一个圆柱体，底面半径为５，高为１０，一只蚂蚁从Ａ点沿外壁爬到Ｂ点，求出蚂蚁爬过的路程？圆柱侧面展开图如果把B点换到下图的位置，你能帮助A点的蚂蚁尽快地爬到B点吗？解：AB=谈谈你在本节课的收获？与同学们分享作业：
2024-09-25
16
100KB
勾股定理的应用——空间最短距离.doc
勾股定理《勾股定理的应用——空间最短距离》一、教学目标1．理解两点之间线段最短；2．掌握几何体不在同一平面上的两点最短距离的寻找方法并求解；3．培养在实际生活中发现问题总结规律的意识和能力。二、重点、难点1．重点：勾股定理应用。2．难点：空间两点间距离的寻找，并构建直角三角形利用勾股定理求解。三、课堂引入先在黑板上任意画两点，请学生找出两点之间的距离，旨在让学生形成最短距离的印象。然后折叠纸张，问：“在一个几何体不同表面的两点，如何寻找最短距离。”引出今天的讨论问题并展示题目所提到的小“蚂蚁”引起学生兴趣
2024-09-23
16
166KB
勾股定理的应用——空间最短距离 (2).pptx
A、B两点间的最短距离是？勾股定理的应用——空间最短距离闯荡几何世界的蚂蚁例1如图边长为1的立方体。蚂蚁从A顶点出发沿着立方体的外表面爬到B顶点的最短路程是如图，边长为1的立方体。蚂蚁从A顶点出发沿着立方体的外表面爬到B顶点的最短路程是问：求空间最短路径的解决思想？例2在长30厘米，宽50厘米，高40厘米的木箱中，蚂蚁在箱内的A处，如果它要在箱壁上爬行到B处，至少要爬多远？ABB总结谢谢！
2024-09-23
16
860KB