正、余弦定理公开课PPT.ppt

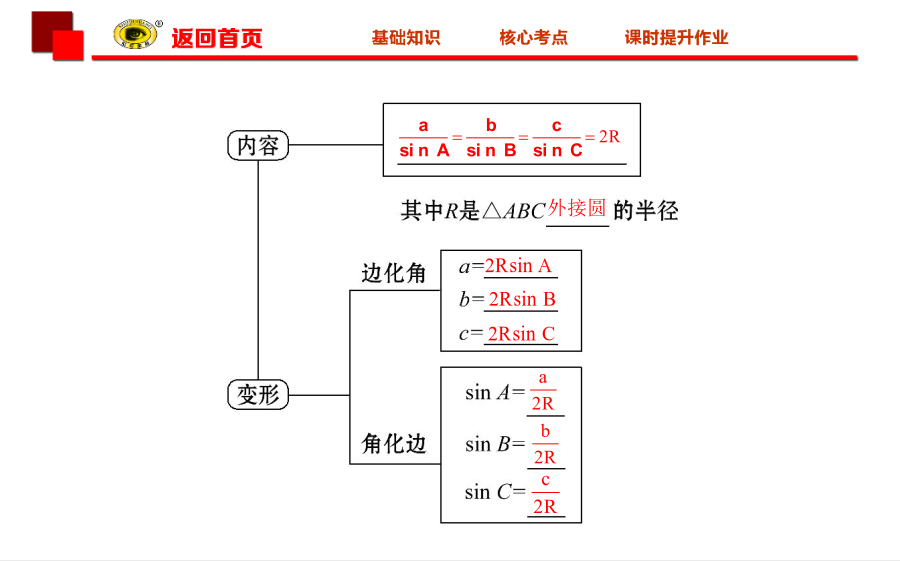
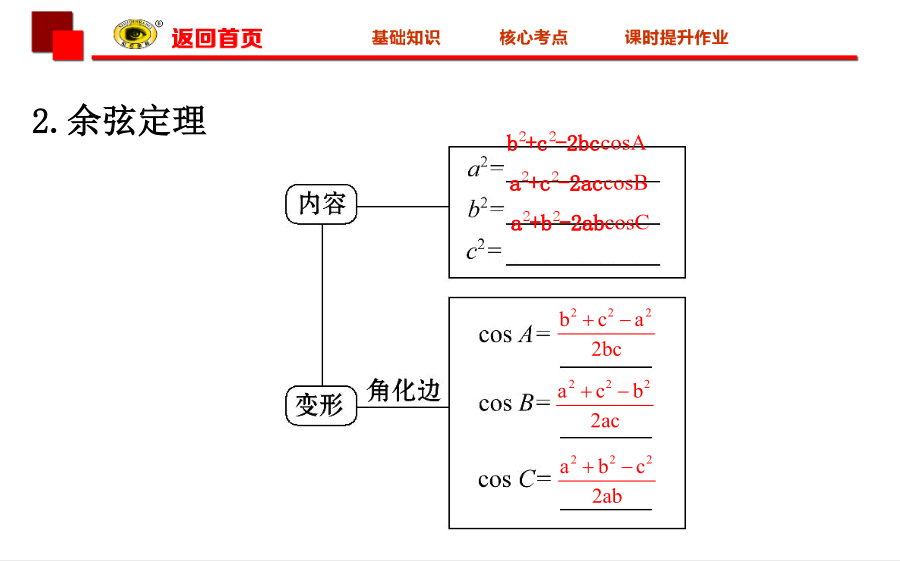
第六节正弦定理和余弦定理（第1课时）【教材知识精梳理】1.正弦定理外接圆2.余弦定理3.三角形的面积公式S△ABC=aha=bhb=chc=_________=_________=_________.【教材拓展微思考】1.在△ABC的六个元素中,已知任意三个元素都可求其他元素吗?提示:已知的三个元素中至少有一条边长,才能求出其他元素.2.在△ABC中,“sinA>sinB”是“A>B”的什么条件?提示:由正弦定理可得,sinA>sinB⇔⇔a>b⇔A>B,所以“sinA>sinB”是“A>B”的充要条件.3.在△ABC中,“b2+c2<a2”是“△ABC为钝角三角形”的什么条件?“b2+c2>a2”是“△ABC为锐角三角形”的什么条件?“b2+c2=a2”是“△ABC为直角三角形”的什么条件?提示:“b2+c2<a2”是“△ABC为钝角三角形”的充分不必要条件,“b2+c2>a2”是“△ABC为锐角三角形”的必要不充分条件.“b2+c2=a2”是“△ABC为直角三角形”的充分不必要条件.【教材母题巧变式】1.在△ABC中,角A,B,C对应的边分别为a,b,c,若A=120°,a=2,b=则B等于()【解析】选D.因为A=120°,a=2,b=所以由正弦定理可得,sinB=sinA因为A=120°,所以B=30°,即B=2.在△ABC中,角A,B,C所对的边分别为a,b,c,若c<bcosA,则△ABC为()A.钝角三角形B.直角三角形C.锐角三角形D.等边三角形【解析】选A.依题意得sinC<sinBcosA,所以sin(A+B)<sinBcosA,即sinBcosA+cosBsinA-sinBcosA<0,所以cosBsinA<0.又sinA>0,于是有cosB<0,B为钝角,△ABC是钝角三角形.3.在△ABC中,a=4,b=5,c=6,则=________.【解析】由余弦定理:cosA=所以所以所以答案:14.在△ABC中,A=60°,AC=4,BC=2,则△ABC的面积等于________.【解析】设△ABC中,角A,B,C对应的边分别为a,b,c.由题意及余弦定理得cosA=解得c=2.所以S=bcsinA=×4×2×sin60°=2.答案:2