
332函数的极值与导数.ppt

qw****27


亲,该文档总共28页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

332函数的极值与导数.ppt
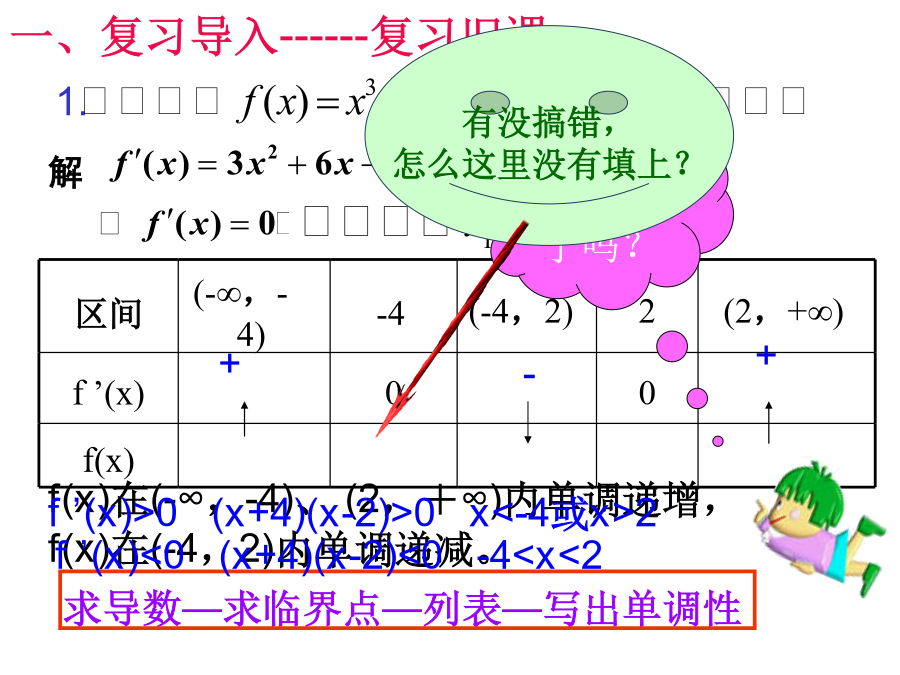
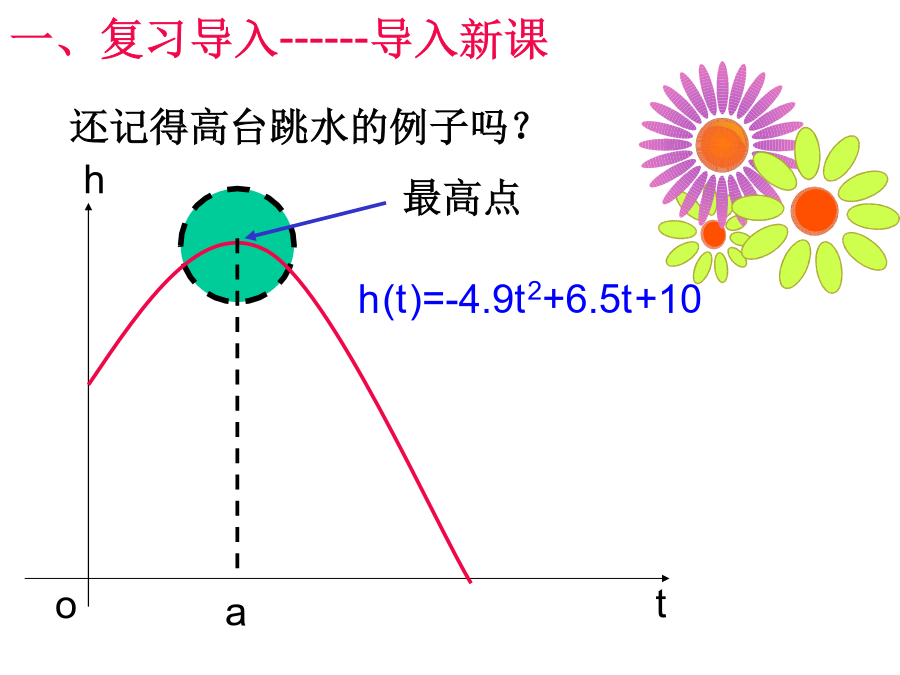
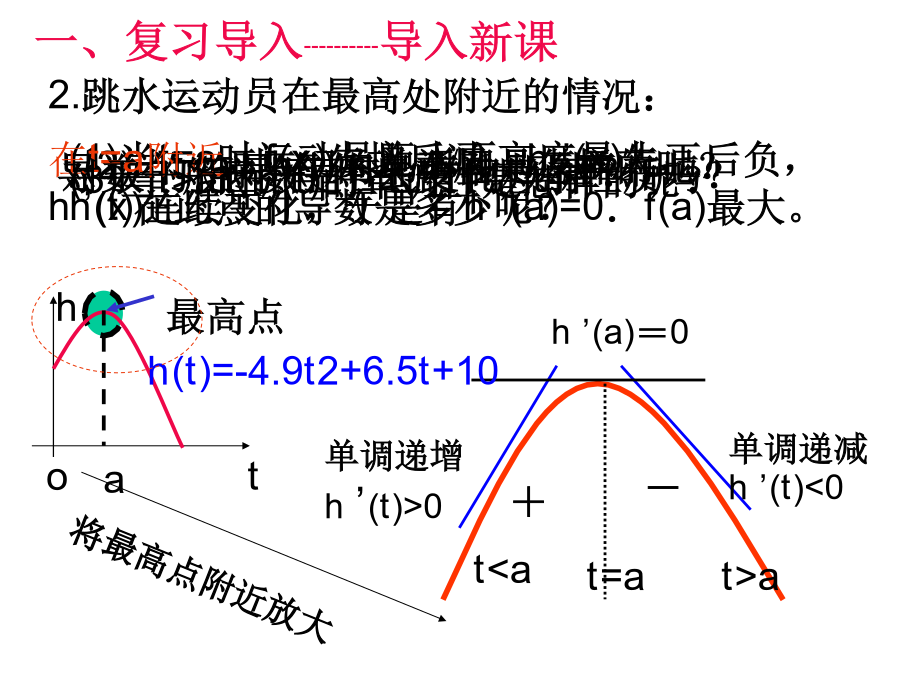
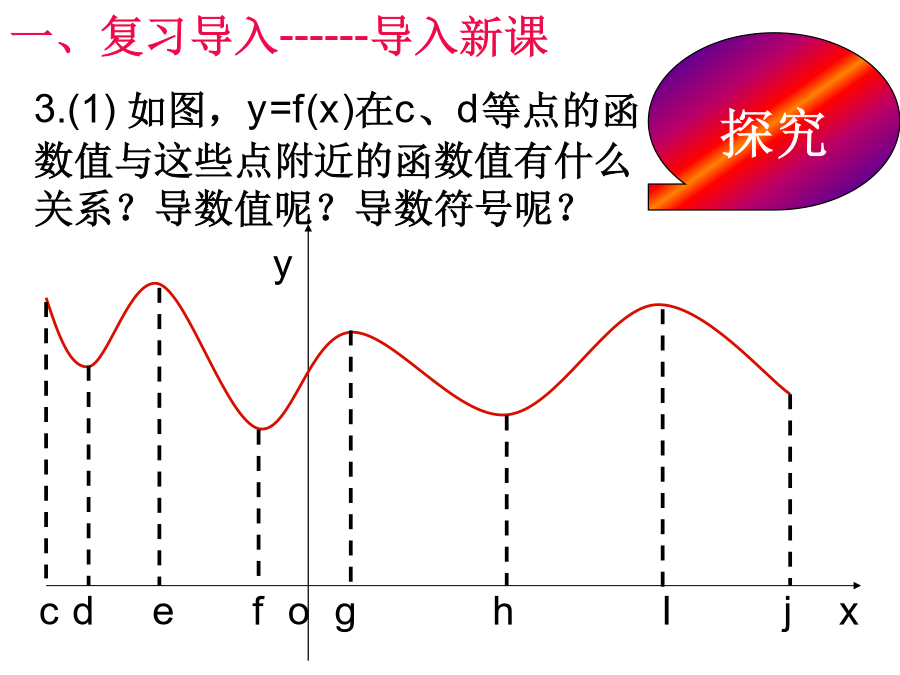
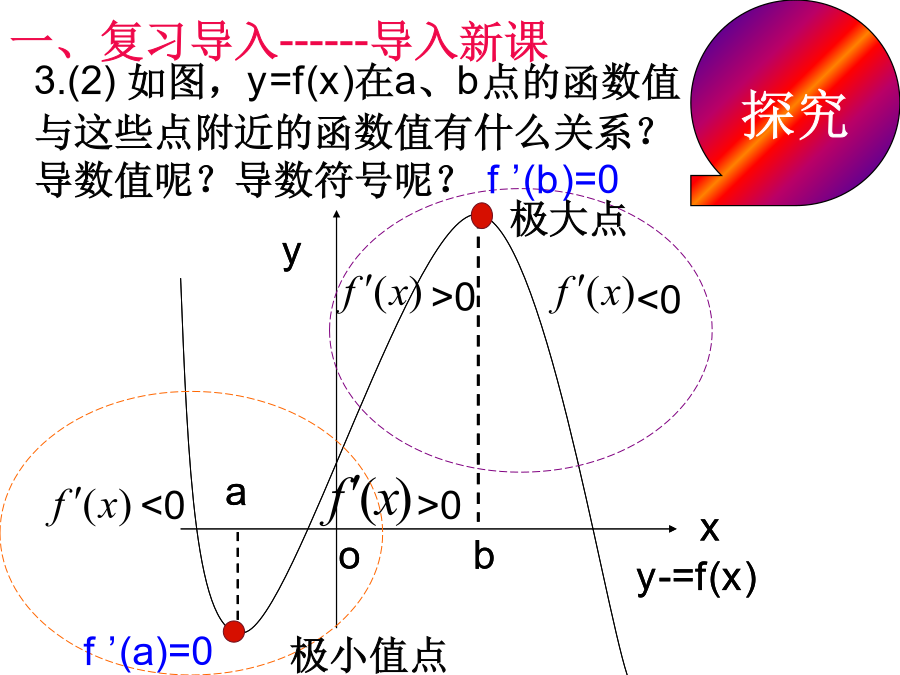
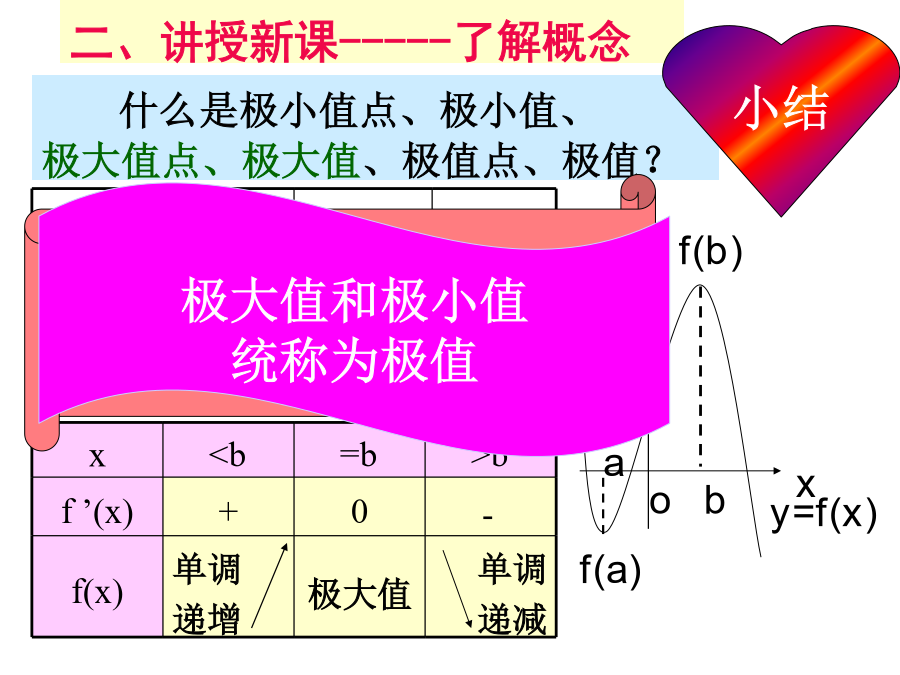
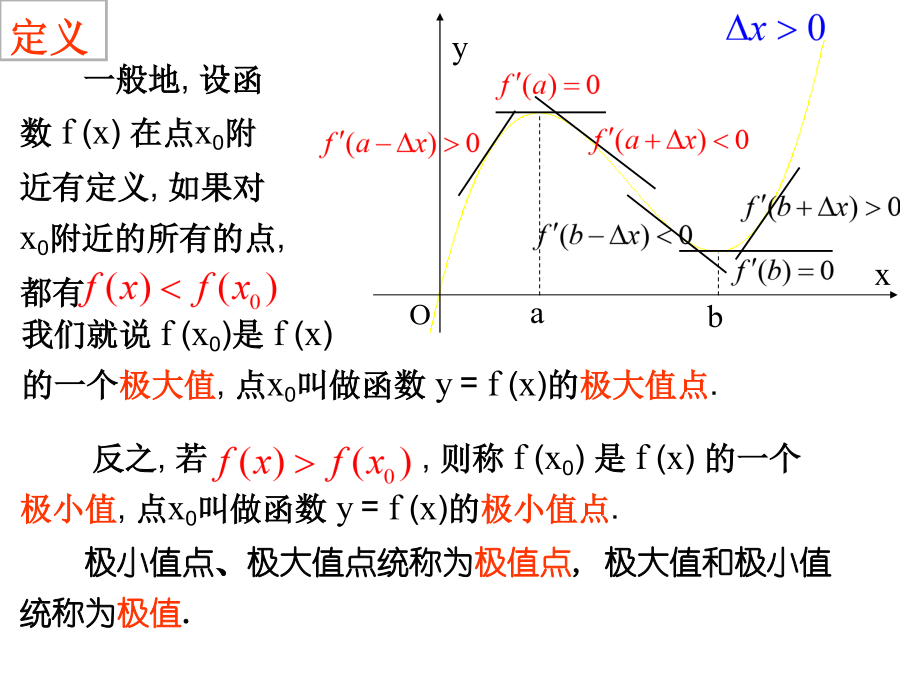
3.3.2函数的极值与导数一、复习导入------复习旧课还记得高台跳水的例子吗?一、复习导入----------导入新课一、复习导入------导入新课一、复习导入------导入新课二、讲授新课-----了解概念a1.理解极值概念时需注意的几点(1)函数的极值是一个局部性的概念,是仅对某一点的左右两侧附近的点而言的.(2)极值点是函数定义域内的点,而函数定义域的端点绝不是函数的极值点.(3)若f(x)在[a,b]内有极值,那么f(x)在[a,b]内绝不是单调函数,即在定义域区间上的单调函数没有极值.(

§332函数的极值与导数.docx
2016-2017学年第一学期高二____年级__数学___学科教案主备人:阿曼古丽·伊斯马伊力所在学校:特高所在年级:高二授课教师:_______________课题§1.3.2函数的极值与导数授课时间2017年3月课时:第二课时课型新授课实际授课时间教学目标知识与技能结合函数图象,了解可导函数在某点取得极值的必要条件和充分条件,理解函数极值的概念,会用导数求函数的极大值与极小值过程与方法结合实例,借助函数图形直观感知,并探索函数的极值与导数的关系。情感态度价值观感受导数在研究函数性质中一般性和有效性,

332函数的极值与导数.ppt
3.3.2函数的极值与导数复习引入题型1.图像与函数的极值题型1.图像与函数的极值题型2.求函数解析式题型2.求函数解析式题型2.求函数解析式题型2.求函数解析式小结ThankYou!

(课件)332函数的极值与导数.ppt
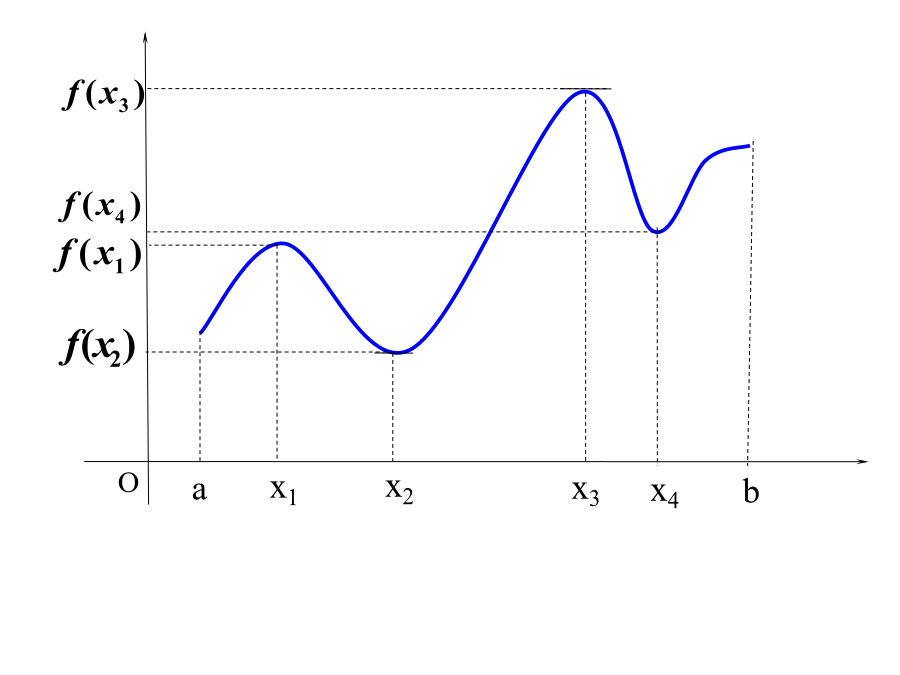
3.3.2函数的极值与导数y一、函数的极值定义y进一步探究:极值点两侧函数图像单调性有何特点?f(x)<0例1:求的极值。变式1求在时极值。例题2:若f(x)=ax3+bx2-x在x=1与x=-1处有极值.(1)求a、b的值(2)求f(x)的极值.小结:注意:函数极值是在某一点附近的小区间内定义的,是局部性质。因此一个函数在其整个定义区间上可能有多个极大值或极小值,并对同一个函数来说,在某一点的极大值也可能小于另一点的极小值。有极大值和极小值,求a范围?

332函数的极值与导数 (2).ppt
3.3.2函数的极值与导数一、复习导入------复习旧课还记得高台跳水的例子吗?一、复习导入----------导入新课一、复习导入------导入新课一、复习导入------导入新课二、讲授新课-----了解概念a1.理解极值概念时需注意的几点(1)函数的极值是一个局部性的概念,是仅对某一点的左右两侧附近的点而言的.(2)极值点是函数定义域内的点,而函数定义域的端点绝不是函数的极值点.(3)若f(x)在[a,b]内有极值,那么f(x)在[a,b]内绝不是单调函数,即在定义域区间上的单调函数没有极值.(
