中考数学专题复习 最值问题解题策略(pdf，无答案) 试题.pdf

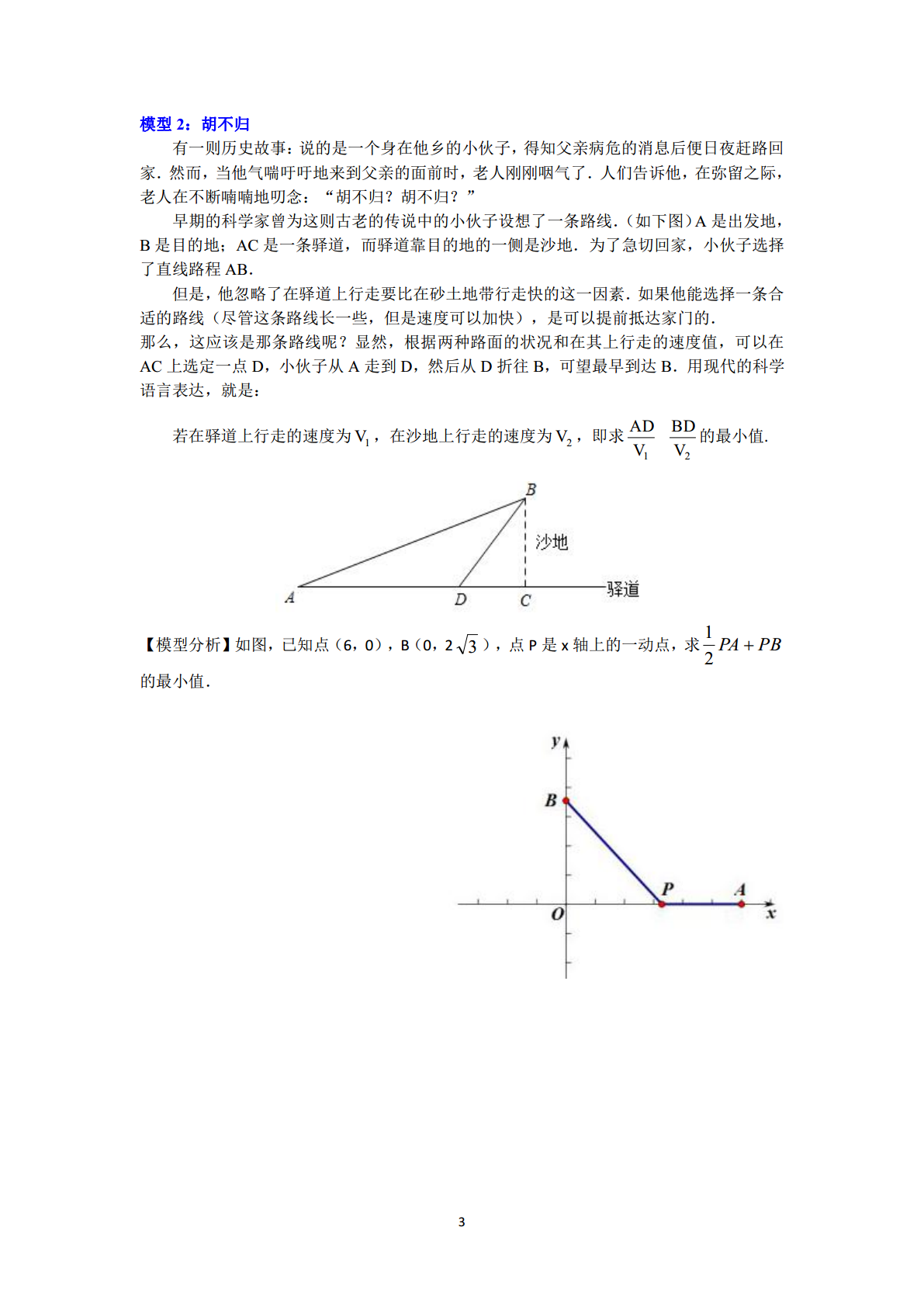
第六学最值问题解题策略【基础要点】初中阶段几何方面求线段的最值问题离不开两句话．让我们一起大声喊出来：两点之间线段最短；垂线段最短．基本模型：将军饮马胡不归阿氏圆．【典型例题】模型1：将军饮马模型介绍：古希腊有一个著名的“将军饮马问题”大致内容如下：古希腊一位将军每天都要巡查河岸侧的两个军营A、B他总是先去A营再到河边饮马之后再去B营如图①他时常想怎么走才能使每天的路程之和最短呢？大数学家海伦曾用轴对称的方法巧妙的解决了这问题如图②作B关于直线l的对称点B′连接AB′与直线l交于点C点C就是所求的位置．请你在下列的阅读、应用的过程中完成解答．（1）理由：如图③在直线L上另取任一点C′连接AC′BC′B′C′∵直线l是点BB′的对称轴点CC′在l上∴CB=C′B=∴AC+CB=AC+CB′=．在△AC′B′中∵AB′＜AC′+C′B′∴AC+CB＜AC′+C′B′即AC+CB最小归纳小结：本问题实际是利用轴对称变换的思想把A、B在直线的同侧问题转化为在直线的两侧从而可利用“两点之间线段最短”即转化为“三角形两边之和大于第三边”的问题加以解决（其中C为AB′与l的交点即A、C、B′三点共线）．本问题可拓展为“求定直线上一动点与直线外两定点的距离和的最小值”问题的数学模型．（2）模型应用[1]如图④正方形ABCD的边长为2E为AB的中点F是AC上一动点．求EF+FB的最小值分析：解决这个问题可以借助上面的模型由正方形的对称性可知B与D关于直线AC对称连结ED交AC于F则EF+FB的最小值就是线段的长度EF+FB的最小值是．[2]如图⑤已知⊙O的直径CD为4∠AOD的度数为60°点B是的中点在直径CD上找一点P使BP+AP的值最小则BP+AP的最小值是；1[3]如图⑥一次函数y=﹣2x+4的图象与xy轴分别交于AB两点点O为坐标原点点C与点D分别为线段OAAB的中点点P为OB上一动点求：PC+PD的最小值并写出取得最小值时P点坐标．图⑦（3）拓展迁移如图⑦已知抛物线y=ax2+bx+c（a≠0）的对称轴为x=1且抛物线经过A（﹣10）、C（0﹣3）两点与x轴交于另一点B．①求这条抛物线所对应的函数关系式；②在抛物线的对称轴直线x=1上找到一点M使△ACM周长最小请求出此时点M的坐标与△ACM周长最小值．（结果保留根号）2（4）代数应用：求代数式x246x36（0≤x≤6）的最小值．2模型2：胡不归有一则历史故事：说的是一个身在他乡的小伙子得知父亲病危的消息后便日夜赶路回家．然而当他气喘吁吁地来到父亲的面前时老人刚刚咽气了．人们告诉他在弥留之际老人在不断喃喃地叨念：“胡不归？胡不归？”早期的科学家曾为这则古老的传说中的小伙子设想了一条路线．（如下图）A是出发地B是目的地；AC是一条驿道而驿道靠目的地的一侧是沙地．为了急切回家小伙子选择了直线路程AB．但是他忽略了在驿道上行走要比在砂土地带行走快的这一因素．如果他