内容提供者
§232平面与平面垂直的判定.ppt
2024-06-11
10金币
1KB
24页
as****16
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
亲，该文档总共24页，到这已经超出免费预览范围，如果喜欢就直接下载吧～
相关资料
232平面与平面垂直的判定.ppt
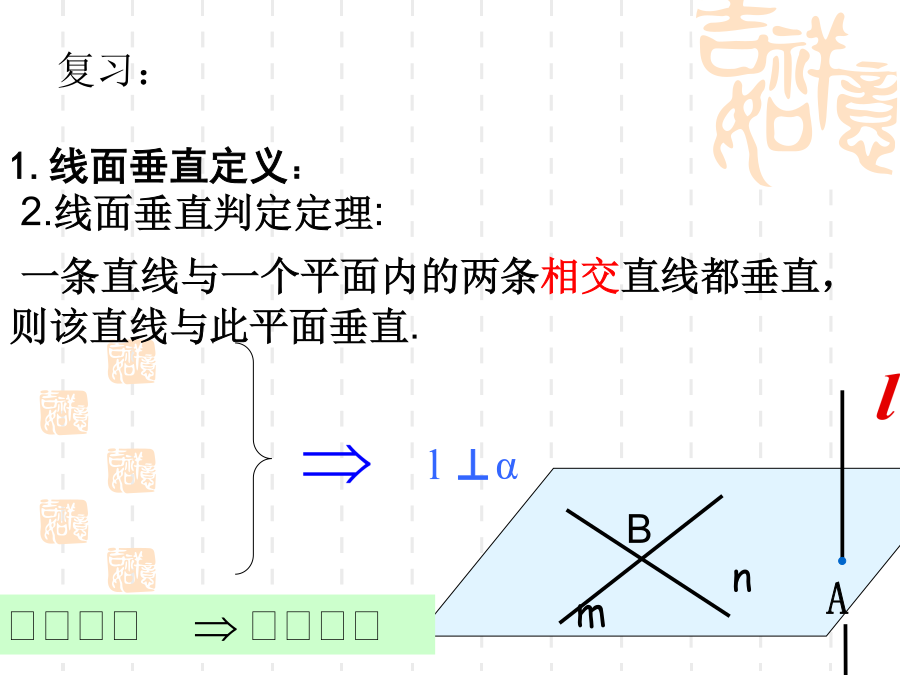
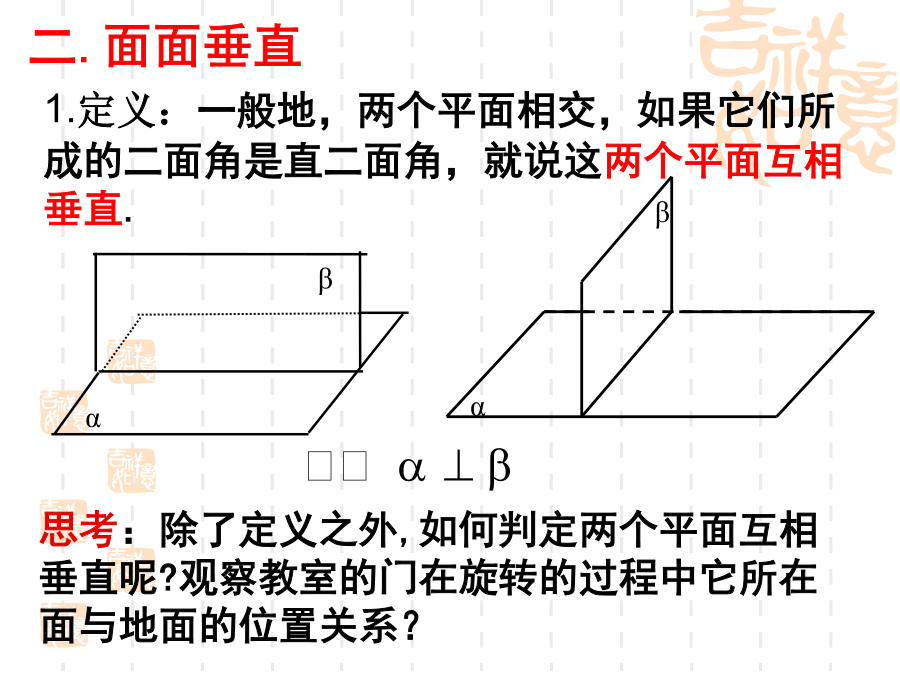
2.3.2平面与平面垂直的判定二面角一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直.平面与平面垂直的判定定理线面垂直判定定理：P76例3探究1：探究1：探究1：探究1：探究1：请问哪些平面互相垂直的,为什么?1、证明面面垂直的方法：作业
2024-06-08
10
677KB
232平面与平面垂直的判定.doc
2.3.2平面与平面垂直的判定衡阳市六中桂婉茹教学目标：1．二面角、平面与平面垂直的概念；2．掌握平面与平面垂直的判定定理，并能利用此定理解决有关问题；3．体验探索过程，学会运用转化化归的数学思想方法。教学重点：平面与平面垂直的判定定理探索。教学难点：平面与平面垂直的判定定理的应用。教学过程：一．引入问题：两个平面有哪几种位置关系？（平行与相交）在生产实践中，有许多问题要涉及到两个平面相交所成的角的情形，你能举出这个问题的一些例子吗？如修水坝、发射人造卫星等，而这样的角有何特点，该如何表示呢？下面我们共同
2024-06-18
10
121KB
232平面与平面垂直的判定.ppt
平面与平面垂直的判定想一想二面角及二面角的平面角l1、二面角的平面角：2、二面角的平面角的作法：一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直.平面与平面垂直的判定定理线面垂直判定定理：探究1：请问哪些平面互相垂直的,为什么?P76例3提高练习：如图：A是ΔBCD所在平面外一点，AB=AD，∠ABC=∠ADC=90°，E是BD的中点，求证：平面AEC⊥平面ABD归纳小结：
2024-06-19
10
867KB
§232平面与平面垂直的判定.ppt
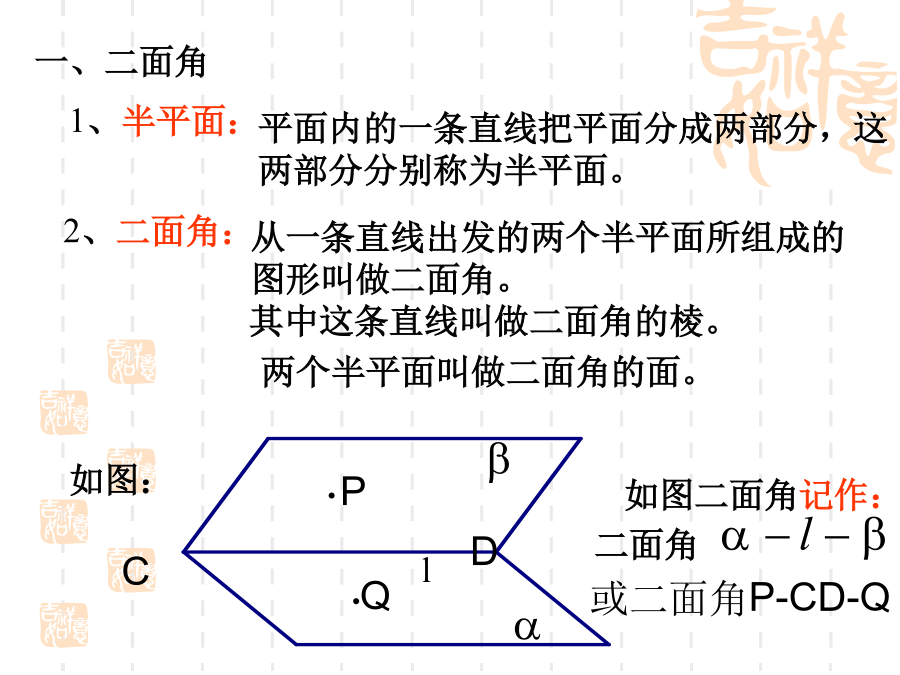
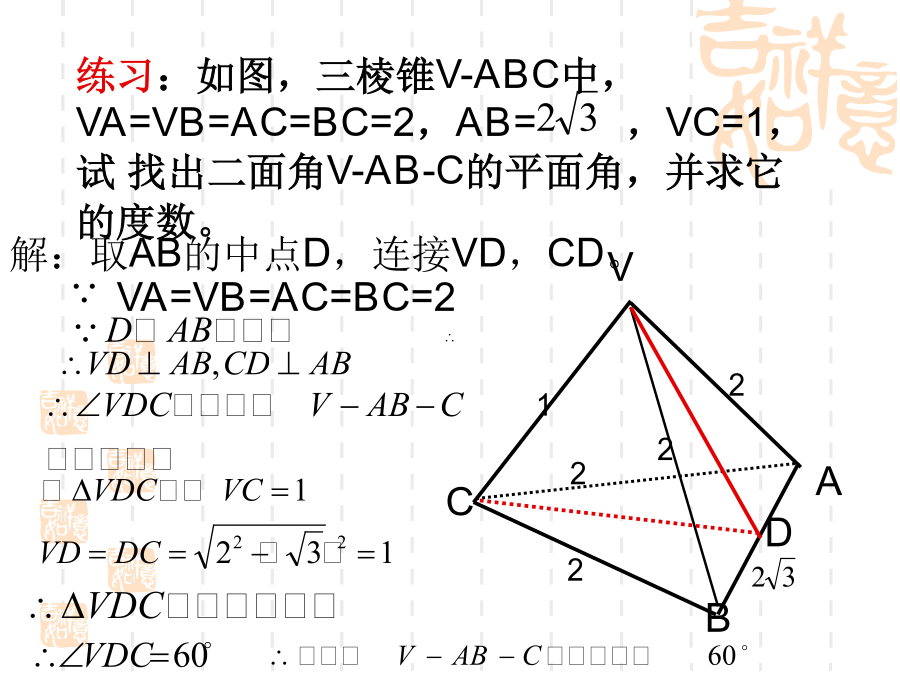
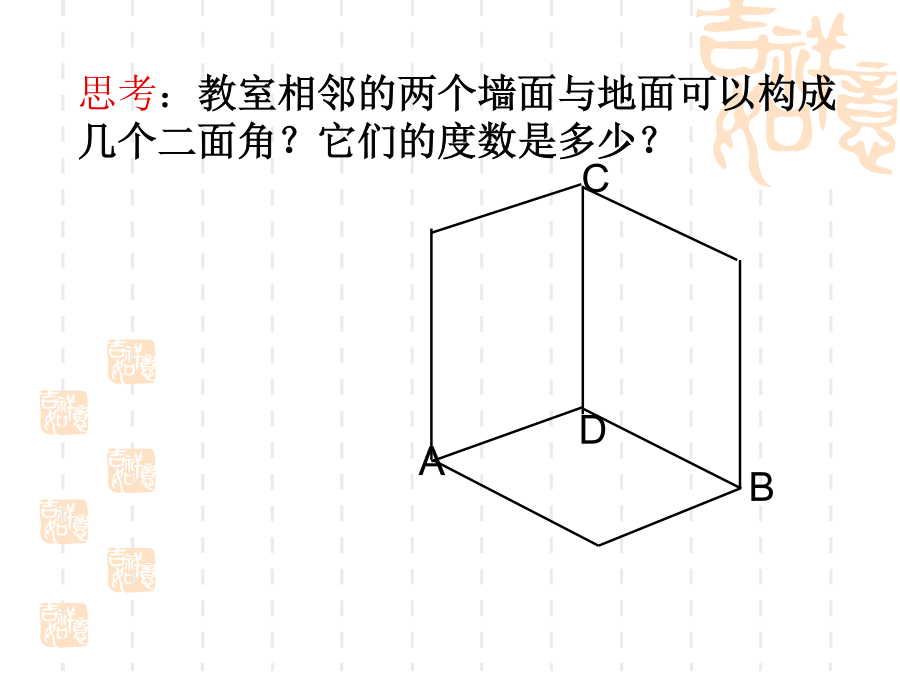
2.3.2平面与平面垂直的判定1.线面垂直定义：一、二面角思考：我们常说“把门开大一些”，是指哪个角大一些？我们应该怎样刻画二面角的大小呢？3、二面角的平面角：练习：如图，三棱锥V-ABC中，VA=VB=AC=BC=2，AB=，VC=1，试找出二面角V-AB-C的平面角，并求它的度数。思考：教室相邻的两个墙面与地面可以构成几个二面角？它们的度数是多少？1.定义：一般地，两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直.2.平面与平面垂直的判定定理探究：探究1：探究1：探究1：例2：如图
2024-06-11
10
1KB
232平面与平面垂直的判定.ppt
2.3.2平面与平面垂直的判定1.使学生正确理解和掌握“二面角”“二面角的平面角”及“直二面角”“两个平面互相垂直”的概念.2.使学生掌握两个平面垂直的判定定理及其简单应用.1.二面角2.二面角的平面角(1)满足条件：如图,二面角α-l-β的平面角为∠AOB,则平面角∠AOB应满足的条件为：①____;②_____;③_____.(2)直二面角：若二面角α-l-β的平面角∠AOB=90°,则该二面角叫做_________.(3)表示方法：图中二面角可记为二面角_______或_____.3.平面与平面垂直
2024-06-04
10
2.9MB