
分形(Fractal)及其在材料科学中的应用.pdf

a是****澜吖






在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

分形(Fractal)及其在材料科学中的应用.pdf
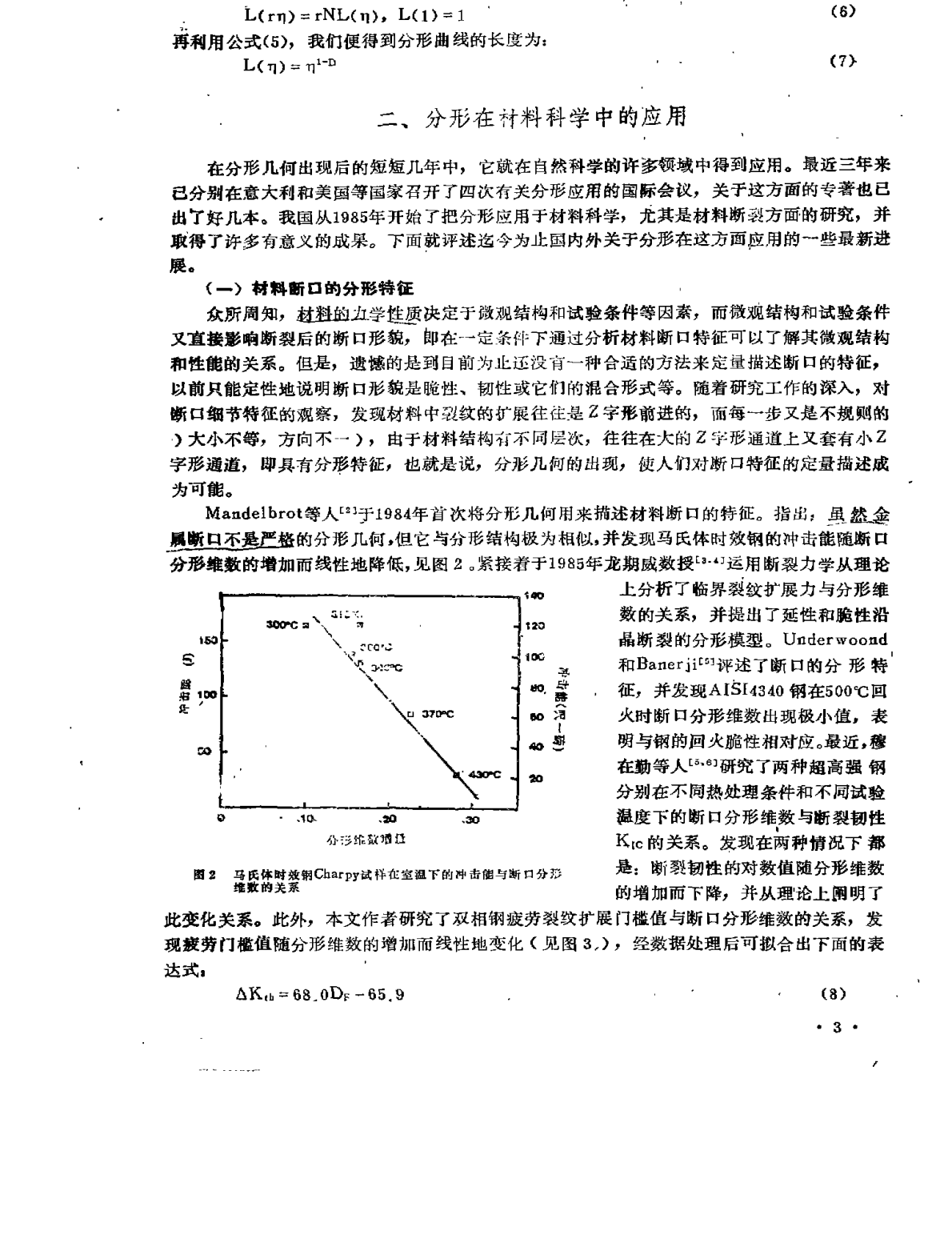
分形及其在材料科学中的应用中国科学院垒属研究所陈道伦.纛●曩】本文简要介绍了近年来出现的一日应用鼓学分支

分形(Fractal)及其在材料科学中的应用.docx
分形(Fractal)及其在材料科学中的应用分形是图形的自相似性质,在材料科学中也有着广泛的应用。本文将介绍分形的概念以及其在材料科学中的应用。一、分形的概念分形,来源于拉丁语“fractus”,意为破碎或零散的。由于分形的自相似性质,一个分形图形可以重复出现于它本身之中,并且在各个尺度上都具有相似的形态特征。例如,树的枝干、闪电、云朵等都具有分形形态。分形的概念不仅仅局限于几何形态,还可以应用于图像、音乐、自然语言等。在材料科学中,分形的应用主要集中在材料的表征和模拟、材料的表面形貌描述、材料的力学特性

分形(fractal)概念及其在化学中的应用.docx
分形(fractal)概念及其在化学中的应用一、分形概念分形是一种几何形态,是指在不同的尺度下成一样或相似的形态的特殊形式,在自然界、科学、经济等领域都有广泛应用。分形体现了自然万物的基本规律,能够通过简单的规则和重复的过程呈现出复杂的形态,因此具有很强的美学和科学价值。分形的研究在数学、物理学、化学、生物学、计算机科学等众多领域取得了广泛的应用,使得我们更加深入地认识到了自然界的奥秘。分形的一大特点是其自相似性。即在一定的尺度下,分形的形态相同或相似。此外,分形具有无限细节、随机性、非整数维度等特点。分

分形(Fractal)理论及在地学中的应用简介.docx
分形(Fractal)理论及在地学中的应用简介分形(Fractal)理论及在地学中的应用分形(Fractal)是一种特殊的几何形态,其指的是一些看似随意扭曲和缩放的图案,但其实它们遵循着一定的自相似性原则。简单来说,从一个分形形状的任何一部分,都能够找到与整体一致的形态。分形理论的提出,为科学家们提供了一种新的思考方式,以及在地学领域中,探究和理解自然景观的重要的视角。分形理论的起源可以追溯到20世纪60年代,那时数学家们开始尝试用理论模型来解释各种自然现象、宇宙规律和生物细胞等复杂系统的规律性。比如自然

分形几何及其在材料科学中的应用.docx
分形几何及其在材料科学中的应用分形几何及其在材料科学中的应用摘要:分形几何是一种几何形态的描述方法,它具有自相似性和无限复杂性的特点。分形几何已经在众多领域中得到广泛应用,其在材料科学中的应用尤为突出。本论文将介绍分形几何的基本原理和特征,并探讨其在材料科学中的应用,如材料的表面形貌描述、颗粒堆积的模拟和分析、材料的力学性能分析等。分子寻踪技术和扫描电镜等先进的实验方法可以用来验证分形几何的有效性。在未来,分形几何在材料科学中的应用将会继续拓展,为材料科学的研究和应用带来更多的突破。关键词:分形几何;自相
