
221对数与对数运算(第1课时).pptx

sy****28









亲,该文档总共11页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

221对数与对数运算第1课时对数.ppt
2.2对数函数2.2.1对数与对数运算第1课时对数把纸沿着中线对折,若要使折得页数为128页,需折多少次?我们研究指数函数时,曾讨论过细胞分裂问题,某种细胞分裂时,由1个分裂成2个,2个分裂成4个…….1个这样的细胞分裂x次后,得到细胞个数y是分裂次数x的函数,这个函数可以用指数函数y=2x,x∈N表示。反过来,1个细胞经过多少次分裂,大约可以得到8个、1024个、8192个……?已知细胞个数为y,如何求分裂次数x?2x=8,x=?2x=1024,2x=8192,x=?1.理解对数的概念;(重点)2.能够

221对数与对数运算(第1课时).pptx
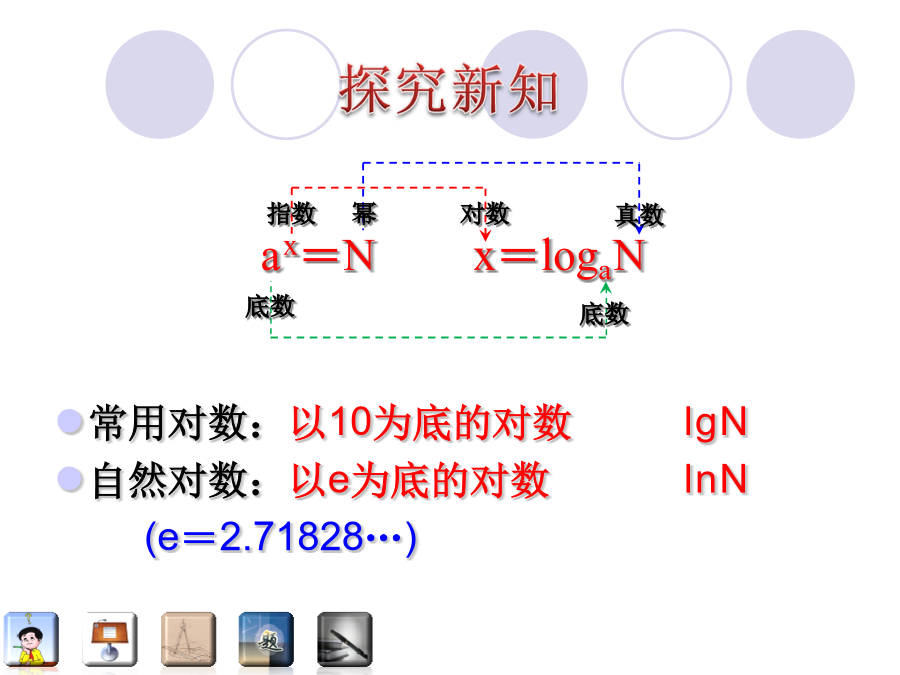
设疑引入设疑引入问题导学:定义一般地,如果ax=N(a>0且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,其中a叫做对数的底数,N叫做真数.ax=N例1:下列各组指数式与对数式互换不正确的是:对数的性质由当a>0且a≠1时,ax=Nx=logaN,且a0=1,a1=a可得:(1)负数和零没有对数;(2)loga1=0;(3)logaa=1.例2:求下列各式中的x值:对数恒等式:a>0且a≠1,N>0反思小结

221对数与对数运算(第1课时).pptx
设疑引入设疑引入问题导学:定义一般地,如果ax=N(a>0且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,其中a叫做对数的底数,N叫做真数.ax=N例1:下列各组指数式与对数式互换不正确的是:对数的性质由当a>0且a≠1时,ax=Nx=logaN,且a0=1,a1=a可得:(1)负数和零没有对数;(2)loga1=0;(3)logaa=1.例2:求下列各式中的x值:对数恒等式:a>0且a≠1,N>0反思小结

221正式对数与对数运算第2课时对数的运算.ppt
第2课时对数的运算底2.对数的性质:已知指数运算法则:1.掌握对数的运算性质,并能理解推导对数运算法则的依据和过程;2.能较熟练地运用法则解决问题.探究:对数的运算性质试一试:由思考2:结合前面的推导,由指数式又能得到什么样的结论?结论:对数的运算性质用表示下列各式:解:例2求下列各式的值:对于底数相同的对数式的化简,常用的方法是:(1)“收”:将同底的两对数的和(差)收成积(商)的对数.(2)“拆”:将积(商)的对数拆成对数的和(差).(1)81.利用对数定义及指数运算法则证明对数的运算法则;2.对数运

221对数与对数运算第2课时对数的运算.ppt
第2课时对数的运算底2.对数的性质:已知指数运算法则:1.理解对数的运算性质;(重点)2.了解对数在简化运算中的作用.探究:对数的运算性质试一试:由思考2:结合前面的推导,由指数式又能得到什么样的结论?结论:对数的运算性质用表示下列各式:解:例2求下列各式的值:对于底数相同的对数式的化简,常用的方法是:(1)“收”:将同底的两对数的和(差)收成积(商)的对数.(2)“拆”:将积(商)的对数拆成对数的和(差).(1)81.对数的运算法则;2.利用定义及指数运算证明对数的运算法则;3.对数运算法则的应用;积、
