垂径定理的应用-豆柴文库

垂径定理的应用.ppt

2024-06-08

10金币

292KB

11页

as****16

实名认证

内容提供者

1/10

2/10

3/10

4/10

5/10

6/10

7/10

8/10

9/10

10/10

亲，该文档总共11页，到这已经超出免费预览范围，如果喜欢就直接下载吧～

下载提示文本预览

如果您无法下载资料，请参考说明：

1、部分资料下载需要金币，请确保您的账户上有足够的金币

2、已购买过的文档，再次下载不重复扣费

3、资料包下载后请先用软件解压，在使用对应软件打开

相关资料

垂径定理.1 垂径定理的应用.ppt

24.1垂径定理的应用乌鲁木齐市第七中学3.如图,在⊙O中弦AB⊥AC,OM⊥AB,ON⊥AC,垂足分别为M,N,且OM=2,0N=3,则AB=,AC=,OA=练一练1、辅助线：连半径、作弦心距小结与思考快乐学习与君共勉

2024-09-26

1.5MB

垂径定理的应用.ppt

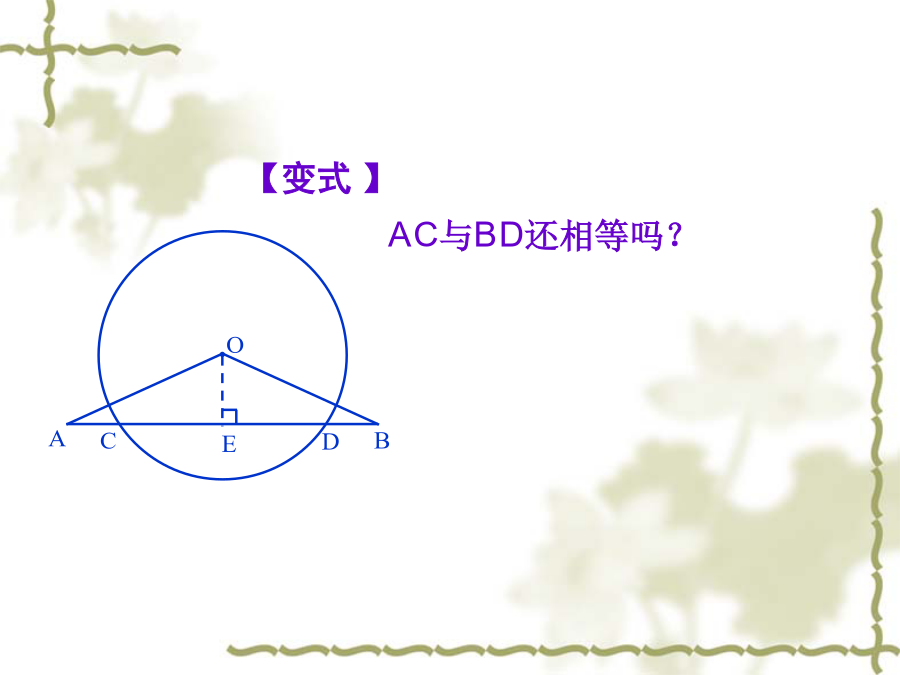
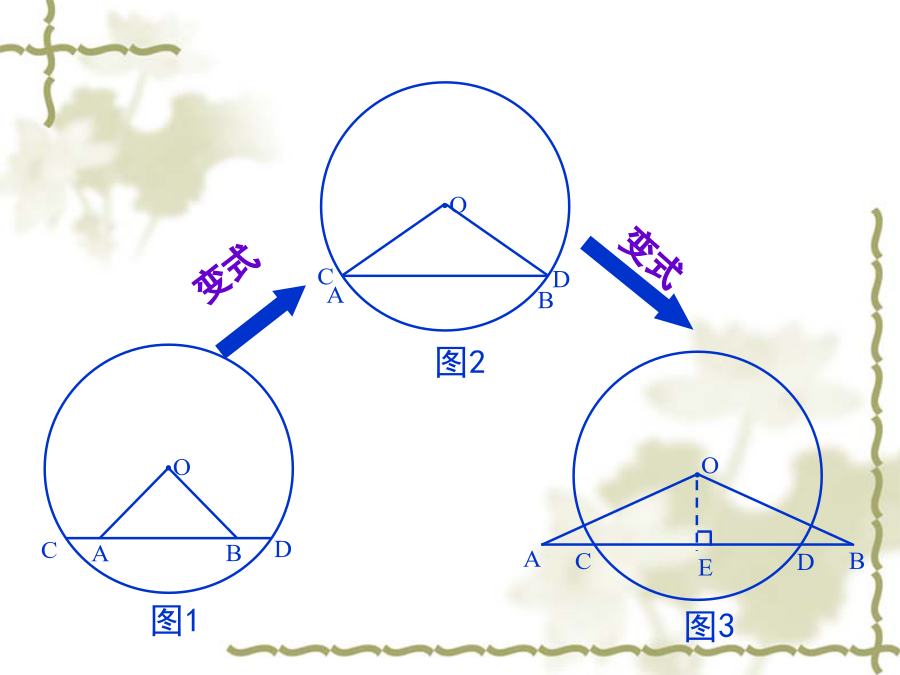
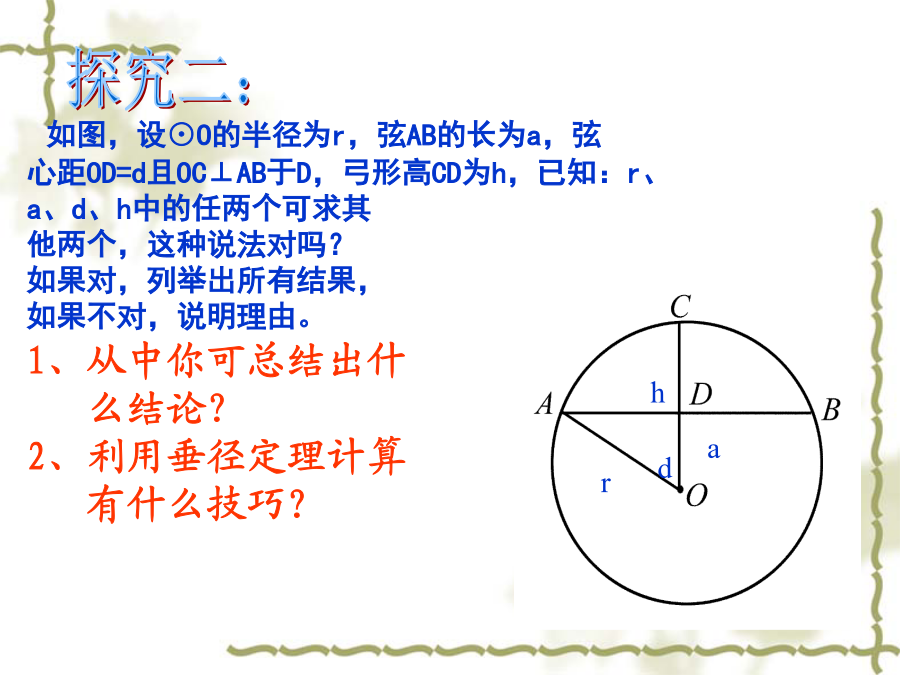
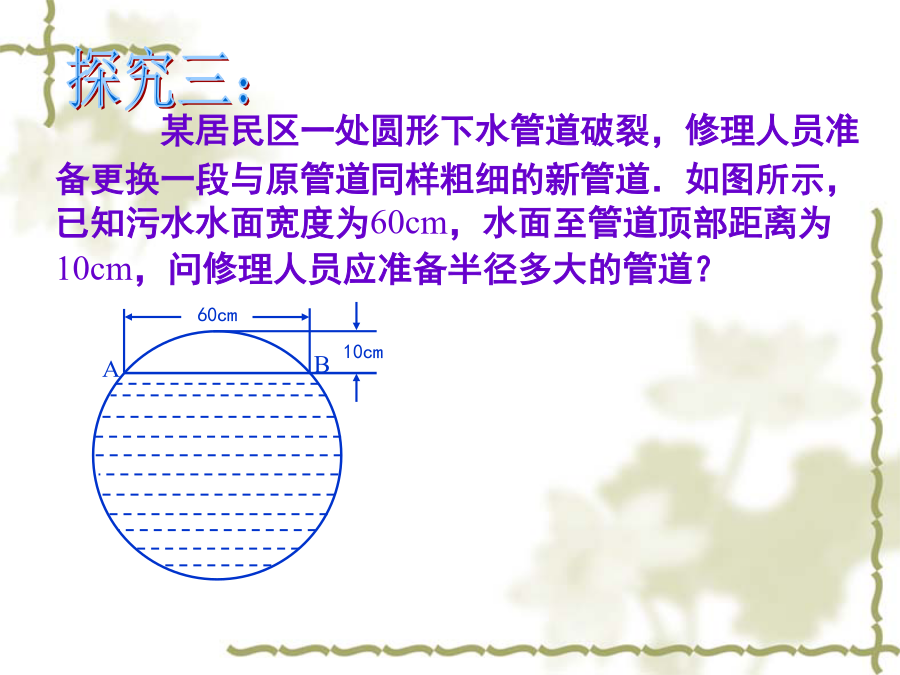
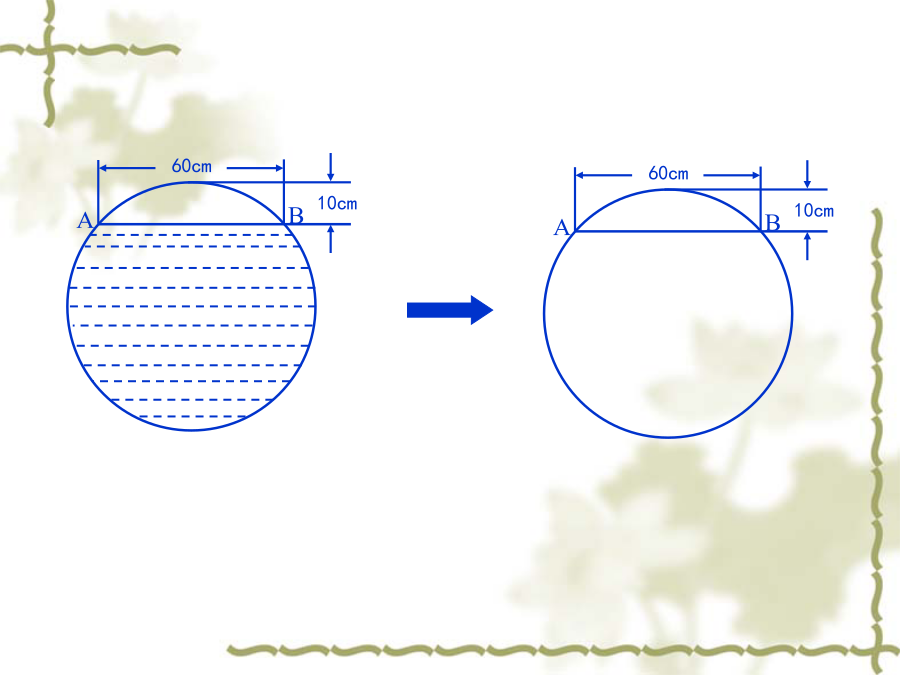
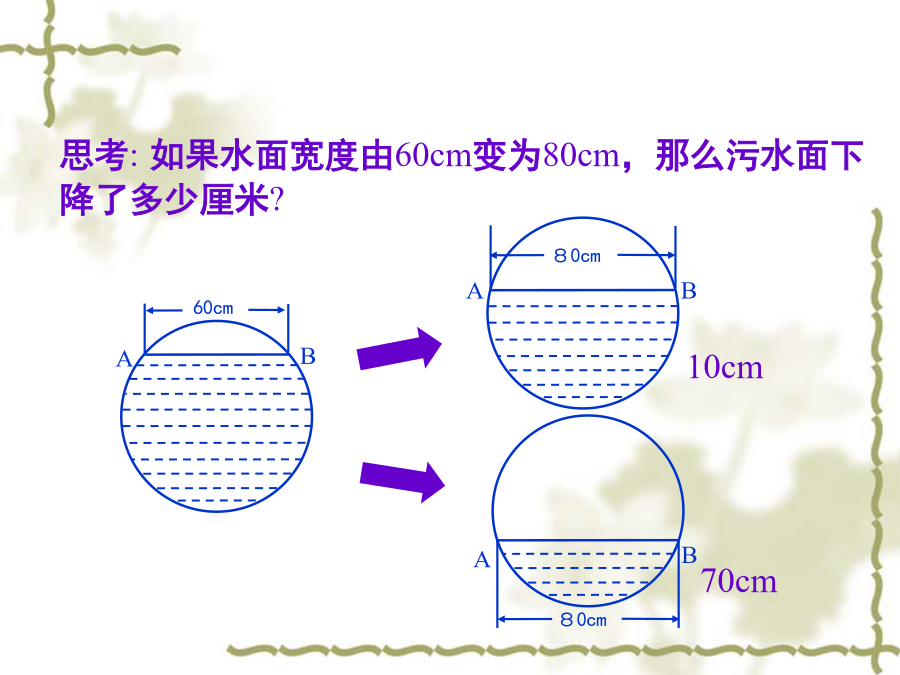
直线AB与⊙O交于C、D两点，且OA＝OB．AC与BD相等吗？说说你的理由．A【变式】A如图，设⊙O的半径为r，弦AB的长为a，弦心距OD=d且OC⊥AB于D，弓形高CD为h，已知：r、a、d、h中的任两个可求其他两个，这种说法对吗？如果对，列举出所有结果，如果不对，说明理由。1、从中你可总结出什么结论？2、利用垂径定理计算有什么技巧？某居民区一处圆形下水管道破裂，修理人员准备更换一段与原管道同样粗细的新管道．如图所示，已知污水水面宽度为60cm，水面至管道顶部距离为10cm，问修理人员应准备半径多大的管

2024-06-08

292KB

垂径定理的应用.ppt

垂径定理的应用垂径定理垂径定理的逆定理垂径定理的逆定理垂径定理三角形2、如图，在⊙O中，AB为⊙O的弦，C、D是直线AB上两点，且AC＝BD求证：△OCD为等腰三角形。垂径定理的应用垂径定理的应用垂径定理的应用赵州石拱桥赵州石拱桥船能过拱桥吗结束寄语

2024-06-07

302KB

垂径定理的应用.ppt

讨论例1300多年前，我国隋朝建造的赵州石拱桥（如图）的桥拱是圆弧形，它的跨度（弧所对是弦的长）为37.4米，拱高（弧的中点到弦的距离，也叫弓形高）为7.2米，求桥拱的半径（精确到0.1米）.赵州桥解：如图，用表示桥拱，所在圆的圆心为O，半径为R米，经过圆心O作弦AB的垂线OD，D为垂足，与相交于点C.根据垂径定理，D是AB的中点，C是的中点，CD就是拱高.由题设练习小结

2024-08-14

204KB

垂径定理的应用.ppt

圆的基本性质复习＿＿垂径定理的运用已知下列命题：①平分弦的直径垂直于弦.②垂直平分弦的直线必定过圆心.③过弦的中点的直线平分弦所对的弧.④弦所对的两条弧的中点连线垂直平分弦，且过圆心.其中正确的有.1、在△ABC中，⊙O是它的外接圆，ODAB于D,OEAC于E.若DE=3,则BC=.2、如图,在⊙O中,点E分别是AO、CD的中点，则四边形OCAD是哪种特殊的四边形？3、如图，⊙O的直径CD与弦AB（非直径）交于点M,添加一个条件：，就可得到AM=BM.题组（二）2、如图,AB为⊙O的直径,E是弧BC的中点

2024-06-24

726KB