
几何最值问题专题.doc

sy****28









在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

几何最值问题专题.doc
几何最值一、常见几何最值问题有:(1)线段最值问题(2)线段和、差最值问题(3)周长最值问题(4)面积问题二、解决几何最值问题的基本原理:(1)两点之间线段最短(2)垂线段最短(3)利用函数知识求几何最值三、练习:1、(2012山东莱芜)在△ABC中,AB=AC=5,BC=6.若点P在边AC上移动,则BP的最小值是.2、(2012四川广元)如图,点A的坐标为(-1,0),点B在直线上运动,线段AB最短时,点B的坐标为(,)3、(2012山东济南)如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM

几何最值问题专题.doc
几何最值一、常见几何最值问题有:(1)线段最值问题(2)线段和、差最值问题(3)周长最值问题(4)面积问题二、解决几何最值问题的基本原理:(1)两点之间线段最短(2)垂线段最短(3)利用函数知识求几何最值三、练习:1、(2012山东莱芜)在△ABC中,AB=AC=5,BC=6.若点P在边AC上移动,则BP的最小值是.2、(2012四川广元)如图,点A的坐标为(-1,0),点B在直线上运动,线段AB最短时,点B的坐标为(,)3、(2012山东济南)如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM
2014专题几何中的最值问题.doc
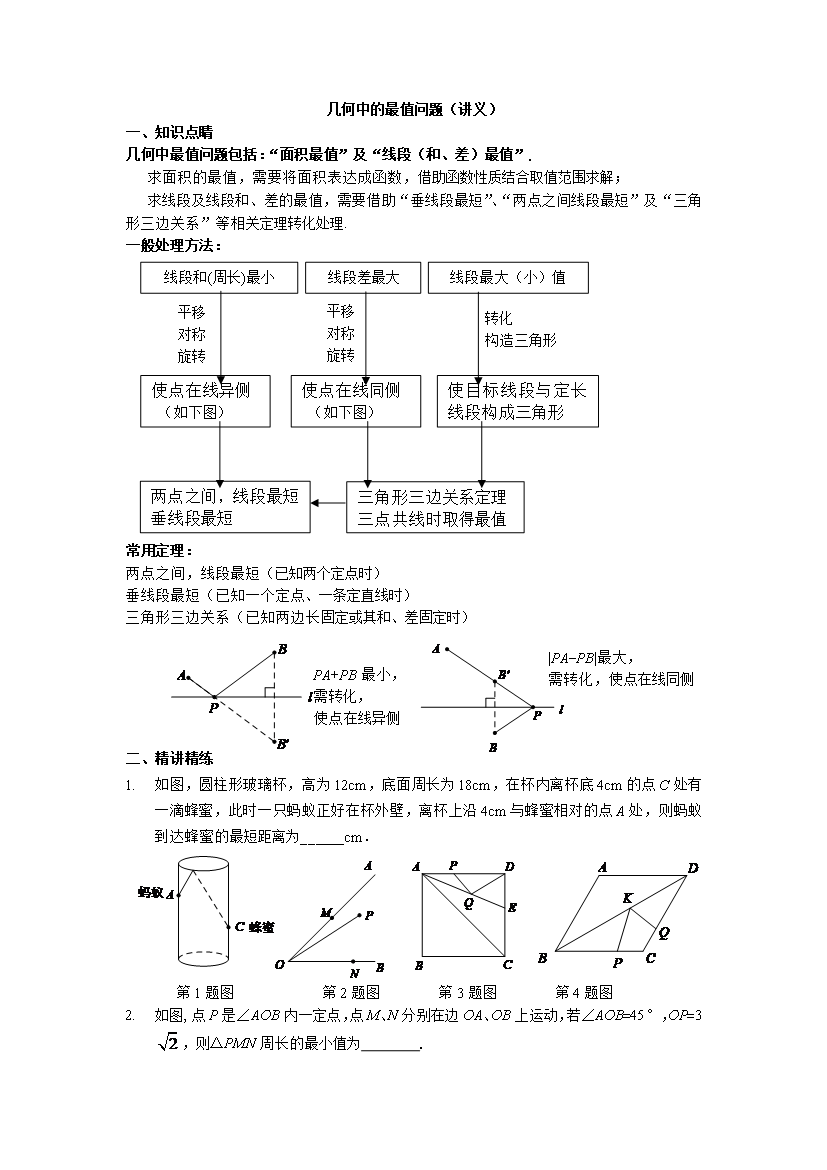
几何中的最值问题(讲义)一、知识点睛几何中最值问题包括:“面积最值”及“线段(和、差)最值”.求面积的最值,需要将面积表达成函数,借助函数性质结合取值范围求解;求线段及线段和、差的最值,需要借助“垂线段最短”、“两点之间线段最短”及“三角形三边关系”等相关定理转化处理.一般处理方法:线段最大(小)值线段差最大线段和(周长)最小平移对称旋转平移对称旋转转化构造三角形使目标线段与定长线段构成三角形使点在线同侧(如下图)使点在线异侧(如下图)三角形三边关系定理三点共线时取得最值两点之间,线段最短垂线段最短常用定
几何中的最值问题专题复习.ppt
几何中的最值问题专题复习1.乌龟与兔子想从点A到点B,走那条路线最短?.根据是.2.如图,污水处理厂要从A处把处理过的水引入排水沟PQ,应如何铺设排水管道,才能使用料最省?试画出铺设管道的路线?并说明理由。3.已知一个三角形玩具的三边长分别为6㎝,8㎝,a㎝,则a的最值范围是.依据:.①两点之间线段最短;②垂线段最短;③三角形的三边关系:三角形两边之差小于第三边,两边之和大于第三边④圆外一点与圆心的连线上,该点和此直线与圆的近交点距离最短、远交点距离最长(2016·福建龙岩)如图,在周长为12的菱形ABC

2014专题几何中的最值问题.doc
几何中的最值问题(讲义)一、知识点睛几何中最值问题包括:“面积最值”及“线段(和、差)最值”.求面积的最值,需要将面积表达成函数,借助函数性质结合取值范围求解;求线段及线段和、差的最值,需要借助“垂线段最短”、“两点之间线段最短”及“三角形三边关系”等相关定理转化处理.一般处理方法:线段最大(小)值线段差最大线段和(周长)最小平移对称旋转平移对称旋转转化构造三角形使目标线段与定长线段构成三角形使点在线同侧(如下图)使点在线异侧(如下图)三角形三边关系定理三点共线时取得最值两点之间,线段最短垂线段最短常用定
