
第31课时——用二分法求方程的近似解.doc

雅云****彩妍




在线预览结束,喜欢就下载吧,查找使用更方便
相关资料
第31课时——用二分法求方程的近似解.doc
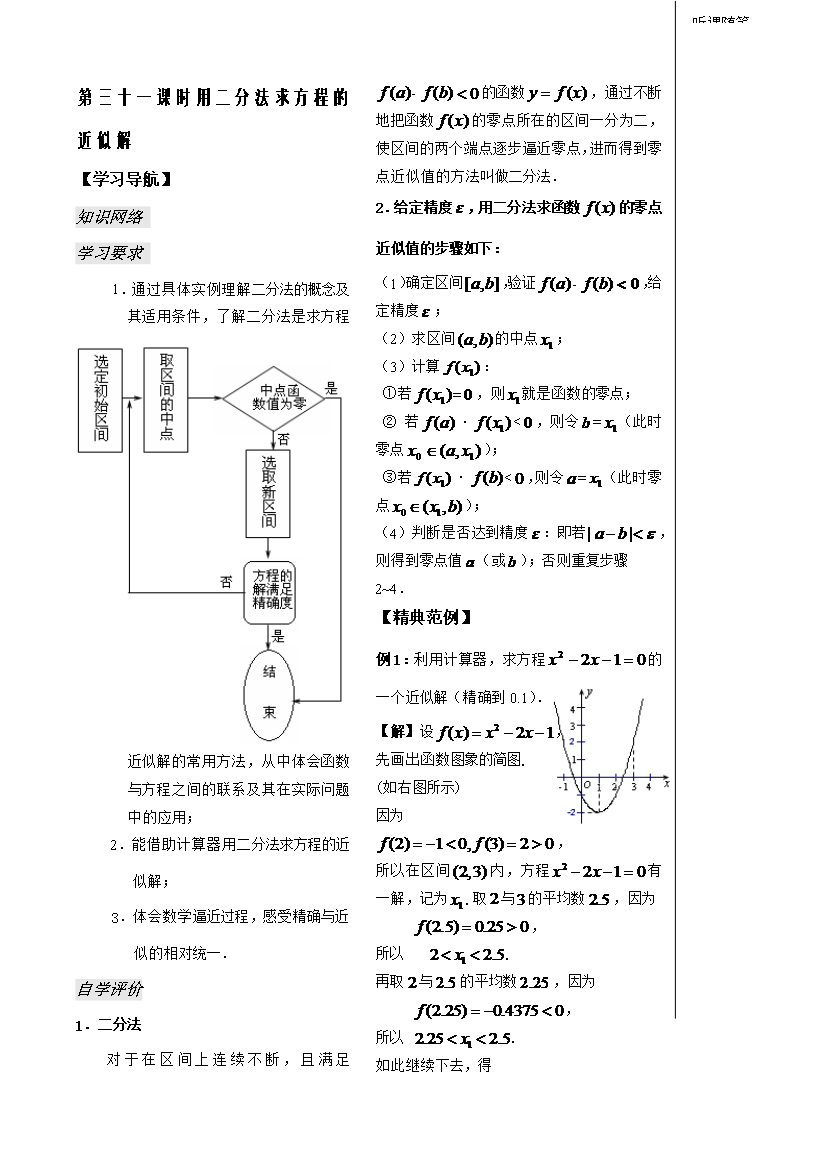
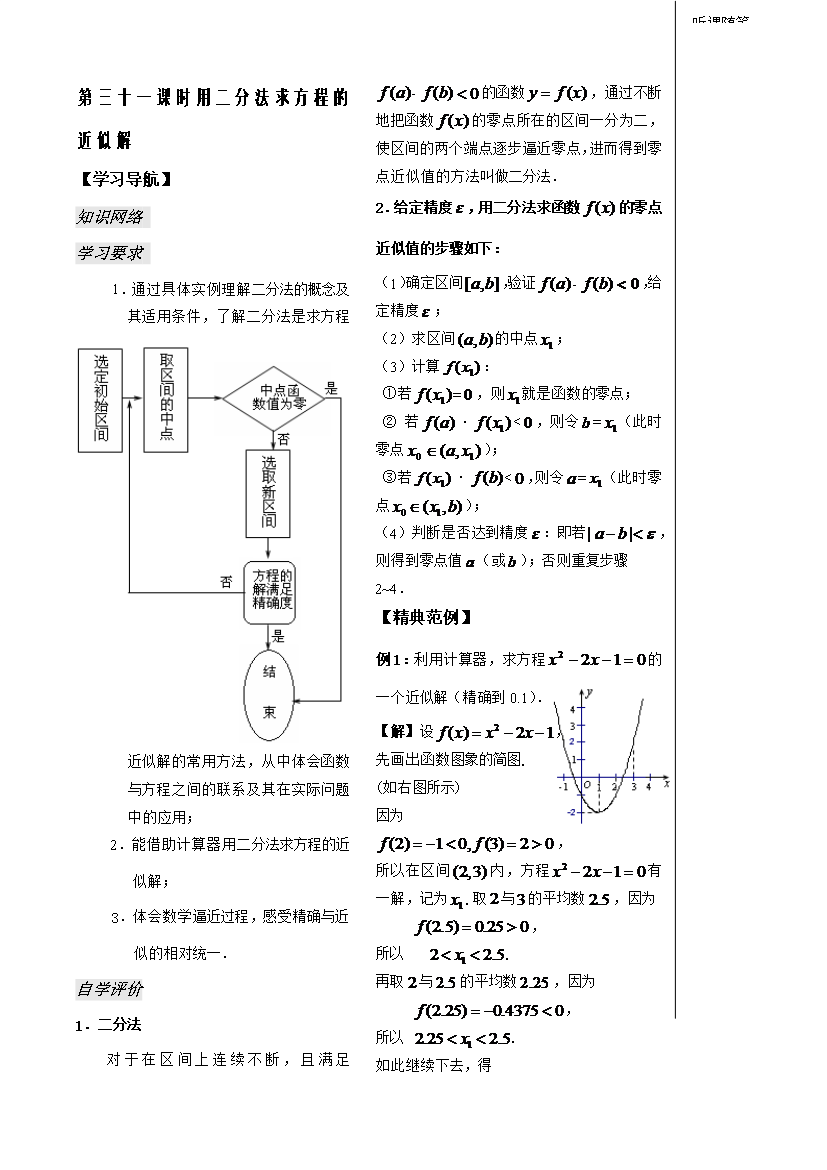
第三十一课时用二分法求方程的近似解【学习导航】知识网络学习要求1.通过具体实例理解二分法的概念及其适用条件了解二分法是求方程近似解的常用方法从中体会函数与方程之间的联系及其在实际问题中的应用;2.能借助计算器用二分法求方程的近似解;3.体会数学逼近过程感受精确与近似的相对统一.自学评价1.二分法对于在区间上连续不断且满足的函数通过不断地把函数的零点所在的区间一分为二使区间的两个端点逐步逼近零点进而得到零点近似值的方法叫做二分法.2.给定精度用二分法求函数的零点近似值的步骤如下:听课随笔(1

第31课时——用二分法求方程的近似解.doc
第三十一课时用二分法求方程的近似解【学习导航】知识网络学习要求1.通过具体实例理解二分法的概念及其适用条件,了解二分法是求方程近似解的常用方法,从中体会函数与方程之间的联系及其在实际问题中的应用;2.能借助计算器用二分法求方程的近似解;3.体会数学逼近过程,感受精确与近似的相对统一.自学评价1.二分法对于在区间上连续不断,且满足的函数,通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.2.给定精度,用二分法求函数的零点近似值的步骤如下:听课随笔(1

第31课时——用二分法求方程的近似解.doc
第三十一课时用二分法求方程的近似解【学习导航】知识网络学习要求1.通过具体实例理解二分法的概念及其适用条件,了解二分法是求方程近似解的常用方法,从中体会函数与方程之间的联系及其在实际问题中的应用;2.能借助计算器用二分法求方程的近似解;3.体会数学逼近过程,感受精确与近似的相对统一.自学评价1.二分法对于在区间上连续不断,且满足的函数,通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.2.给定精度,用二分法求函数的零点近似值的步骤如下:听课随笔(1
第31课时——用二分法求方程的近似解.doc
第三十一课时用二分法求方程的近似解【学习导航】知识网络学习要求1.通过具体实例理解二分法的概念及其适用条件了解二分法是求方程近似解的常用方法从中体会函数与方程之间的联系及其在实际问题中的应用;2.能借助计算器用二分法求方程的近似解;3.体会数学逼近过程感受精确与近似的相对统一.自学评价1.二分法对于在区间上连续不断且满足的函数通过不断地把函数的零点所在的区间一分为二使区间的两个端点逐步逼近零点进而得到零点近似值的方法叫做二分法.2.给定精度用二分法求函数的零点近似值的步骤如下:听课随笔(1

第31课用二分法求方程的近似解.doc
第31课用二分法求方程的近似解1.D2.B3.D4.5.6.C7.A8.9.设.〔1〕由解得.〔2〕由题意可知∴解得.10.设依题意得∴∴.故当时原方程的两实根在区间内.11.令那么方程有实根等价于直线与抛物线的图象有交点而函数的值域为∴。12.解法一:在同一坐标系中分别画出两个函数和的图象.如以下图所示欲使解区间恰为那么直线必过点那么.解法二:∵当时那么.∴那么∴.当时原不等式的解为与题意不符∴舍去.综上知.第32课函数与方程小结与复习
