内容提供者
高中数学 1.3.1函数的极值与导数课件 新人教A版选修2-2.ppt
2024-06-07
10金币
363KB
10页
仙人****88
实名认证
内容提供者
1/10
2/10
3/10
4/10
5/10
6/10
7/10
8/10
9/10
10/10
在线预览结束，喜欢就下载吧，查找使用更方便
相关资料
高中数学 1.3.1函数的极值与导数课件 新人教A版选修2-2.ppt
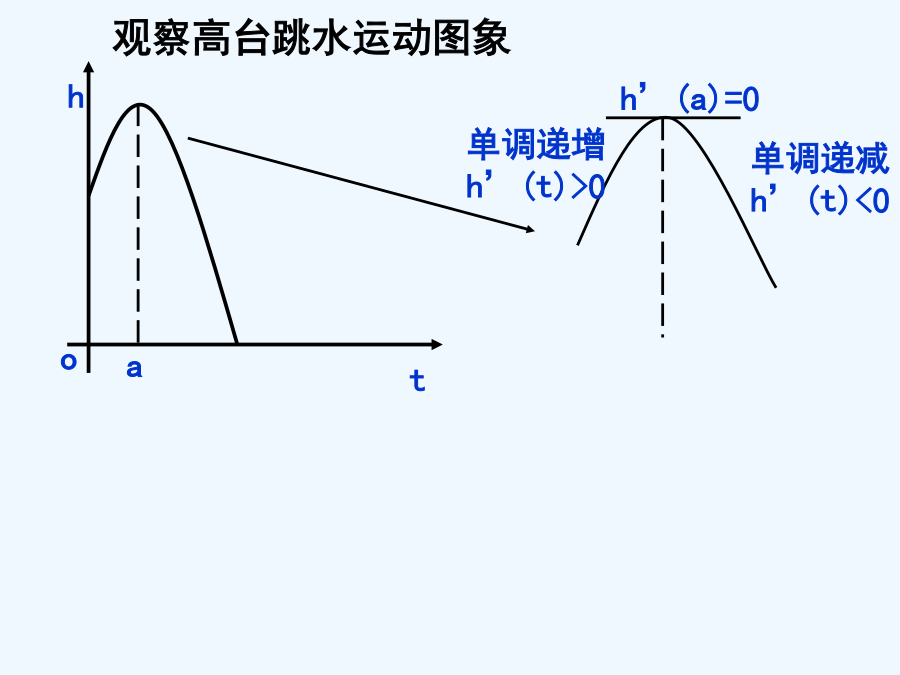
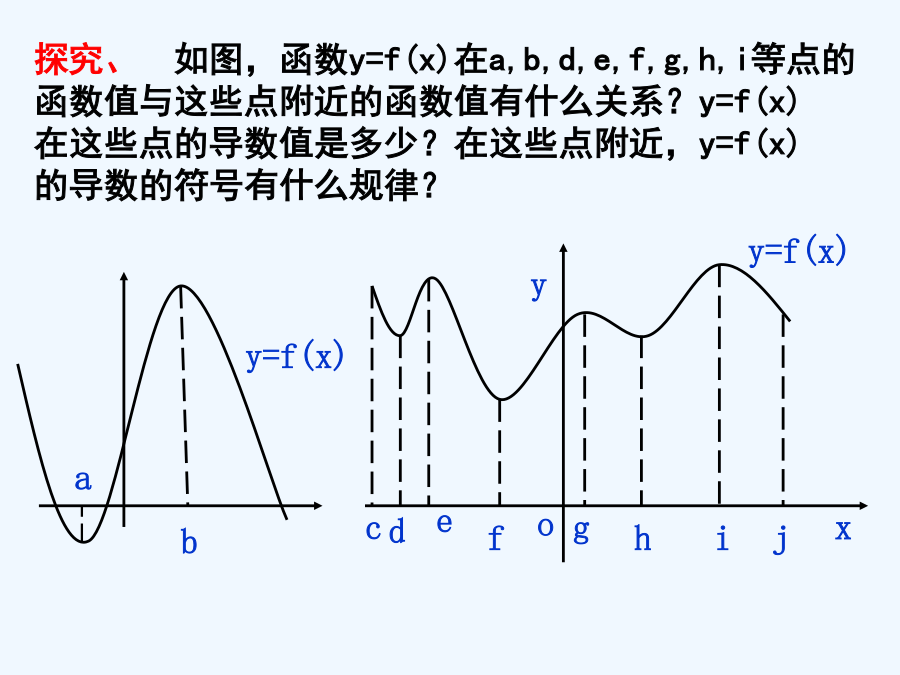
(1.3.2)函数的极值与导数判断函数单调性的常用方法：（1）定义法（2）导数法注、单调区间不以“并集”出现。t探究、如图，函数y=f(x)在a,b,d,e,f,g,h,i等点的函数值与这些点附近的函数值有什么关系？y=f(x)在这些点的导数值是多少？在这些点附近，y=f(x)的导数的符号有什么规律？2)函数y=f(x)在x=b处的函数值f(b)比它在点x=b附近其它各点的函数值都大，我们就说f(b)是函数的一个极大值，点b叫做极大值点．2)如果a是f’(x)=0的一个根，并且在a的左侧附近f’(x)<0
2024-06-07
10
363KB
高中数学 函数的极值与导数课件 新人教A选修22.ppt
3.3.2函数的极值与导数2.求函数单调性的一般步骤关注用导数本质及其几何意义解决问题二、新课讲解——函数的极值:从而我们得出结论:若x0满足f/(x)=0且在x0的两侧的导数异号则x0是f(x)的极值点f(x0)是极值并且如果f/(x)在x0两侧满足“左正右负”则x0是f(x)的极大值点f(x0)是极大值;如果f/(x)在x0两侧满足“左负右正”则x0是f(x)的极小值点f(x0)是极小值.极大值与极小值统称为极值.三、例题选讲:四.探索思考:
2023-12-08
10
362KB
32函数的极值与导数课件(新人教A版选修1-1).ppt
3.3.2函数的极值与导数巩固：y函数的极值定义（1）函数的极值是就函数在某一点附近的小区间而言的，在函数的整个定义区间内可能有多个极大值或极小值1．理解极值概念时需注意的几点(1)函数的极值是一个局部性的概念，是仅对某一点的左右两侧附近的点而言的．(2)极值点是函数定义域内的点，而函数定义域的端点绝不是函数的极值点．(3)若f(x)在[a，b]内有极值，那么f(x)在[a，b]内绝不是单调函数，即在定义域区间上的单调函数没有极值．(4)极大值与极小值没有必然的大小关系．一个函数在其定义域内可以有许多个极
2024-07-02
10
596KB
高中数学 1.3.1函数的单调性与导数课件 新人教A版选修2-2.ppt
1.3.1函数的单调性与导数o函数y=f(x)在给定区间G上，当x1、x2∈G且x1＜x2时(1)函数的单调性也叫函数的增减性；1)如果恒有f′(x)>0，那么y=f（x)在这个区间（a,b)内单调递增；例1、已知导函数的下列信息：例2.确定函数在哪个区间是减函数？在哪个区间上是增函数？利用导数讨论函数单调的步骤:练习：确定函数，在哪个区间是增函数，那个区间是减函数。例3:确定函数f(x)=x/2+sinx;的单调区间:练习:判断下列函数的单调性-1例4:设f(x)=ax3+x恰有三个单调区间,试确定a的
2024-06-07
10
579KB
高中数学 函数的极值与导数课件 新人教A版选修2-2 课件.ppt
3.3.2函数的极值与导数2.求函数单调性的一般步骤关注用导数本质及其几何意义解决问题二、新课讲解——函数的极值:从而我们得出结论:若x0满足f/(x)=0且在x0的两侧的导数异号则x0是f(x)的极值点f(x0)是极值并且如果f/(x)在x0两侧满足“左正右负”则x0是f(x)的极大值点f(x0)是极大值;如果f/(x)在x0两侧满足“左负右正”则x0是f(x)的极小值点f(x0)是极小值.极大值与极小值统称为极值.三、例题选讲:四.探索思考:
2023-06-23
10
962KB