
高二数学下9.5 空间向量及其运算3教案.doc

春波****公主




在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

高二数学下9.5 空间向量及其运算3教案.doc
课题:95空间向量及其运算(三)教学目的:⒈了解空间向量基本定理及其推论;⒉理解空间向量的基底、基向量的概念.理解空间任一向量可用空间不共面的三个已知向量唯一线性表出⒊学会用发展的眼光看问题认识到事物都是在不断的发展、变化的会用联系的观点看待事物.教学重点:向量的分解(空间向量基本定理及其推论)教学难点:空间作图.授课类型:新授课课时安排:1课时教具:多媒体、实物投影仪教学过程:一、复习引入:1.空间向量的概念:在空间我们把具有大小和方向的量叫做向量注:⑴空间的一个平移就是一个

高二数学下9.5 空间向量及其运算教案.doc
课题:95空间向量及其运算(一)教学目的:1.理解空间向量的概念,掌握空间向量的加法、减法和数乘运算2.用空间向量的运算意义和运算律解决立几问题教学重点:空间向量的加法、减法和数乘运算及运算律教学难点:用向量解决立几问题授课类型:新授课课时安排:1课时教具:多媒体、实物投影仪内容分析:本节,空间向量及其运算共有4个知识点:空间向量及其线性运算、共线向量与共面向量、空间向量的分解定理、两个向量的数量积这一节是全章的重点,有了第一大节空间平行概念的基础,我们就很容易把平面向量及其运算推广到空间向量由于本教材学
高二数学下9.5 空间向量及其运算2教案.doc
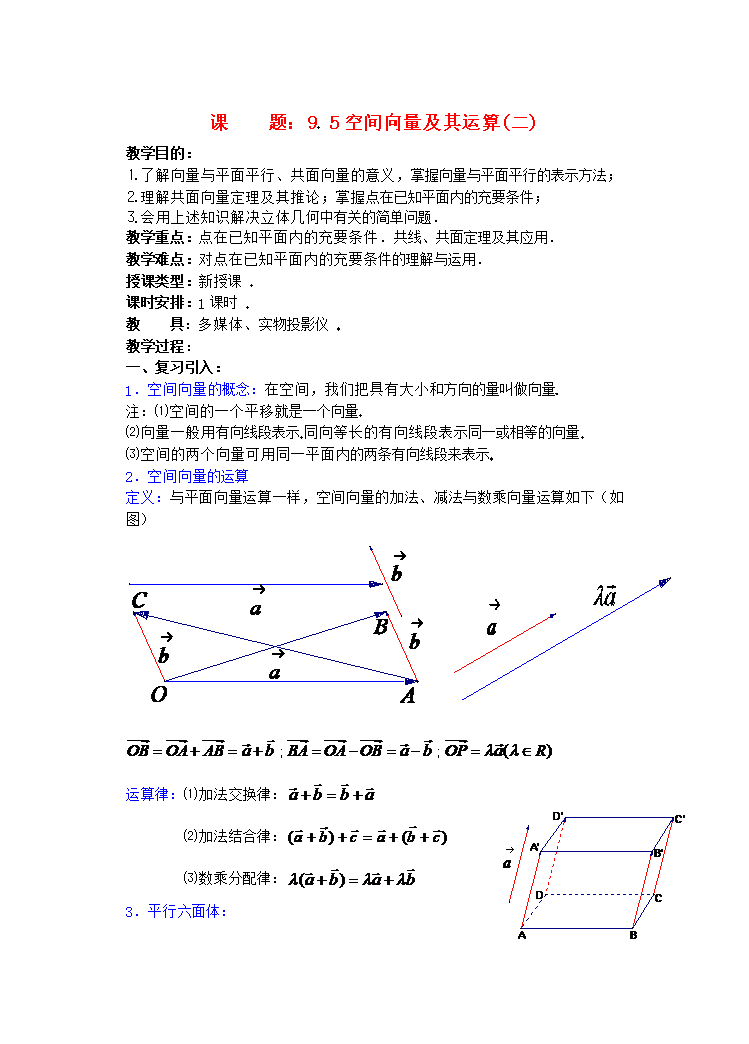
课题:95空间向量及其运算(二)教学目的:⒈了解向量与平面平行、共面向量的意义掌握向量与平面平行的表示方法;⒉理解共面向量定理及其推论;掌握点在已知平面内的充要条件;⒊会用上述知识解决立体几何中有关的简单问题.教学重点:点在已知平面内的充要条件.共线、共面定理及其应用.教学难点:对点在已知平面内的充要条件的理解与运用.授课类型:新授课课时安排:1课时教具:多媒体、实物投影仪教学过程:一、复习引入:1.空间向量的概念:在空间我们把具有大小和方向的量叫做向量注:⑴空间的一个平移就是一

(中小学教案)高二数学下9.5 空间向量及其运算3教案.doc
课题:95空间向量及其运算(三)教学目的:⒈了解空间向量基本定理及其推论;⒉理解空间向量的基底、基向量的概念.理解空间任一向量可用空间不共面的三个已知向量唯一线性表出⒊学会用发展的眼光看问题,认识到事物都是在不断的发展、变化的,会用联系的观点看待事物.教学重点:向量的分解(空间向量基本定理及其推论)教学难点:空间作图.授课类型:新授课课时安排:1课时教具:多媒体、实物投影仪教学过程:一、复习引入:1.空间向量的概念:在空间,我们把具有大小和方向的量叫做向量注:⑴空间的一个平移就是一个向量⑵向量一般用有向线

高二数学9.5空间向量及其运算(一) 教案.doc
课题:95空间向量及其运算(一)教学目的:1.理解空间向量的概念掌握空间向量的加法、减法和数乘运算2.用空间向量的运算意义和运算律解决立几问题教学重点:空间向量的加法、减法和数乘运算及运算律教学难点:用向量解决立几问题授课类型:新授课课时安排:1课时教具:多媒体、实物投影仪内容分析:本节空间向量及其运算共有4个知识点:空间向量及其线性运算、共线向量与共面向量、空间向量的分解定理、两个向量的数量积这一节是全章的重点有了第一大节空间平行概念的基础我们就很容易把平面向量及其运算
