
变式训练专题教案516.doc

仙人****88




在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

变式训练专题教案516.doc
变式训练专题教学设计一、教学目标1.使学生经历变式训练的探索过程,了解数学内容的本质,明确知识之间的相互联系,激活学生的联想和再创造能力。2.通过观察和探索,使学生经历观察、猜测、推理、交流、反思等理性思维基本过程,培养问题意识及运用数学思想方法解决问题的能力。3.培养学生主动探索、勇于发现、敢于实践和合作交流的习惯。二、教学重、难点1.在解题中分析、观察、根据需要选择运用数形结合、分类讨论、化归和转化等基本的数学思想。2.树立整体思想和运动变化观点,能从多角度考虑问题,理顺解题思路,设计解题方案,尽量做

变式训练专题.docx
变式训练专题教学设计一、教学目标1.使学生经历变式训练的探索过程,了解数学内容的本质,明确知识之间的相互联系,激活学生的联想和再创造能力。2.通过观察和探索,使学生经历观察、猜测、推理、交流、反思等理性思维基本过程,培养问题意识及运用数学思想方法解决问题的能力。3.培养学生主动探索、勇于发现、敢于实践和合作交流的习惯。二、教学重、难点1.在解题中分析、观察、根据需要选择运用数形结合、分类讨论、化归和转化等基本的数学思想。2.树立整体思想和运动变化观点,能从多角度考虑问题,理顺解题思路,设计解题方案,尽量做

变式训练专题.ppt
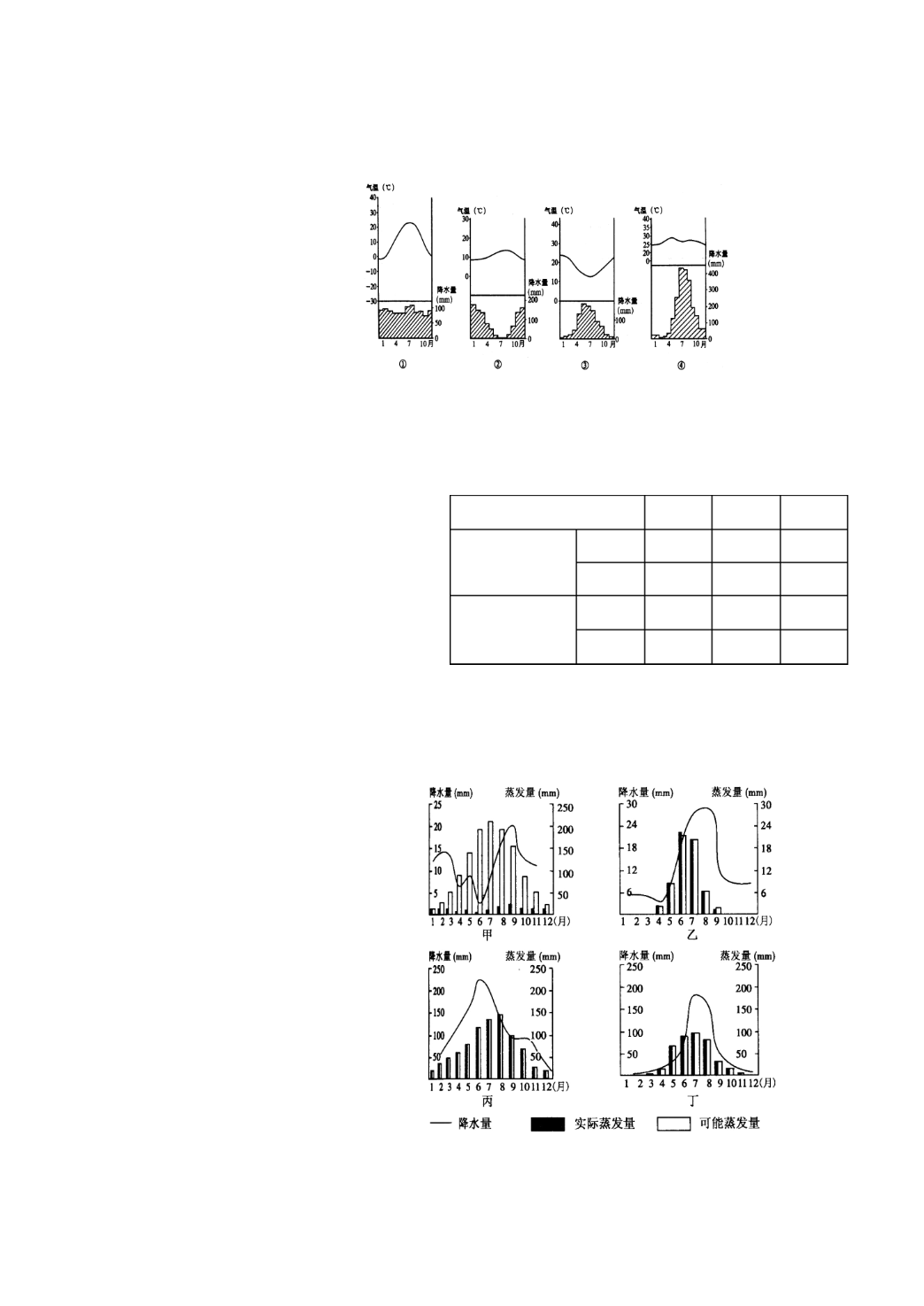
气候变式图专题训练题.pdf

气候变式图专题训练题.doc
希望大家能多支持我们的网站(特价淘宝店www.tjtbd.com),我们会不断奉献各类优质实用的高考复习资料希望大家能多支持我们的网站(特价淘宝店www.tjtbd.com),我们会不断奉献各类优质实用的高考复习资料气候变式图专题训练题如图表示世界四个地点的气温降水状况。读图回答下面四题。1.位于热带气候区的地点是A.①B.②C.③D.④2.位于南半球的地点是A.①B.②C.③D.④3.位于地中海气候区的地点是A.①②B.②③C.③④D.④①4.位于中高纬度大陆东岸的地点是A
