
第三章、CADCAM建模技术.ppt

仙人****88







亲,该文档总共95页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

第三章、CADCAM建模技术.ppt
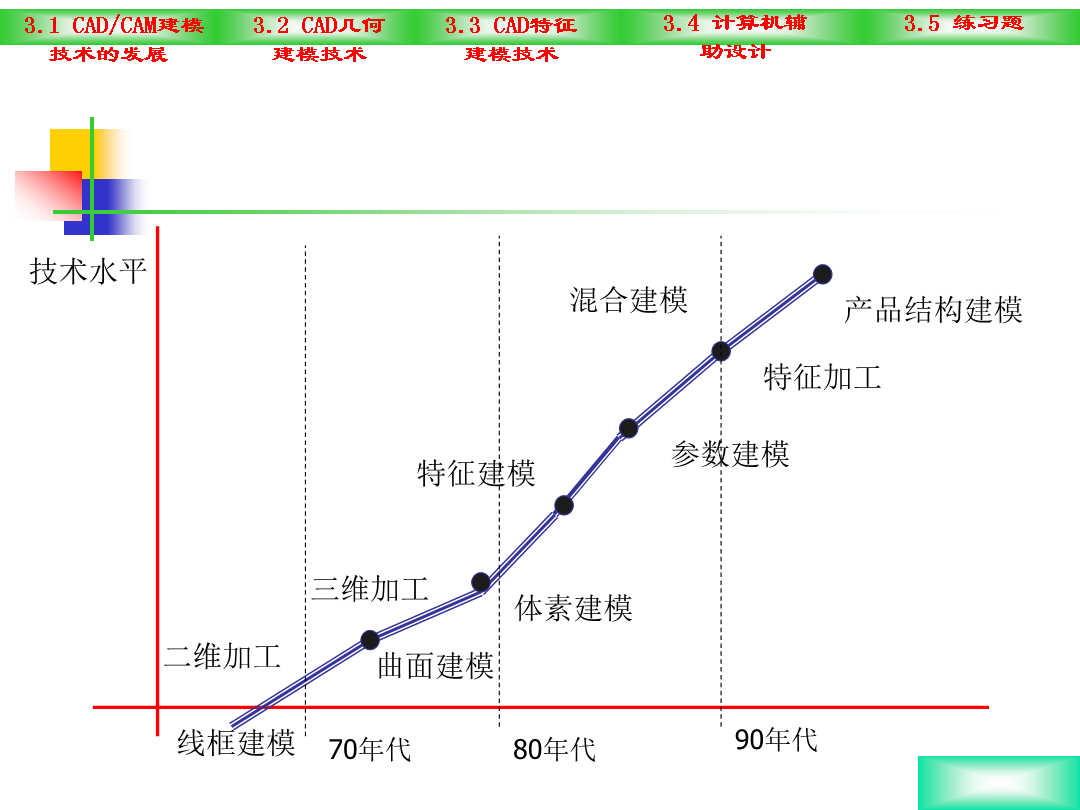
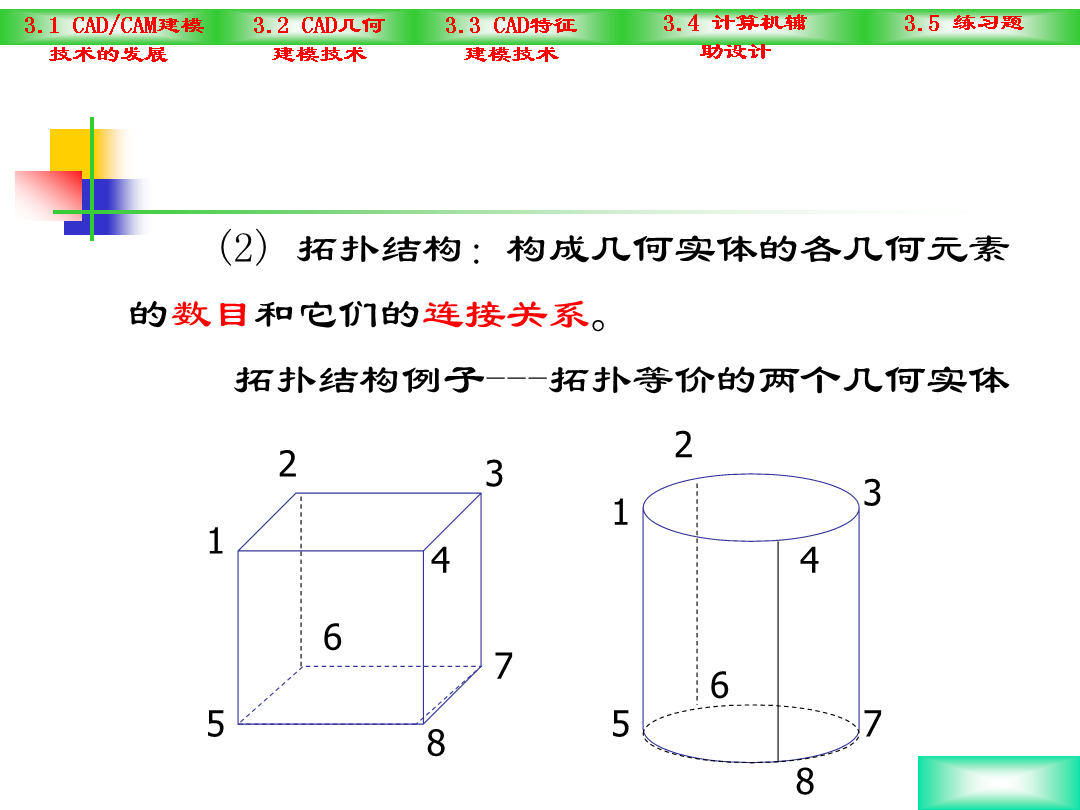
第三章CAD/CAM建模技术3.1CAD/CAM建模技术的发展线框建模几何建模:◆20世纪60年代:线框模型,仅能处理简单的二维、三维图形;◆70年代中期:曲面模型,对复杂表面的设计和制造。◆70年代后期:实体模型,描述单一零件的基本信息有了基础。BUILD系统、PADL系统、TIPS系统等。◆80年代后期:正则集理论;非正则集理论;非均匀有理B样条技术。特征造型技术3.1.2建模技术的发展趋势3.2CAD几何建模技术3.2.1基本概念(2)拓扑结构:构成几何实体的各几何元素的数目和它们的连接关系。拓扑结

第三章、CADCAM建模技术.ppt
第三章CAD/CAM建模技术3.1CAD/CAM建模技术的发展线框建模几何建模:◆20世纪60年代:线框模型,仅能处理简单的二维、三维图形;◆70年代中期:曲面模型,对复杂表面的设计和制造。◆70年代后期:实体模型,描述单一零件的基本信息有了基础。BUILD系统、PADL系统、TIPS系统等。◆80年代后期:正则集理论;非正则集理论;非均匀有理B样条技术。特征造型技术3.1.2建模技术的发展趋势3.2CAD几何建模技术3.2.1基本概念(2)拓扑结构:构成几何实体的各几何元素的数目和它们的连接关系。拓扑结

机械CADCAM建模技术.pptx
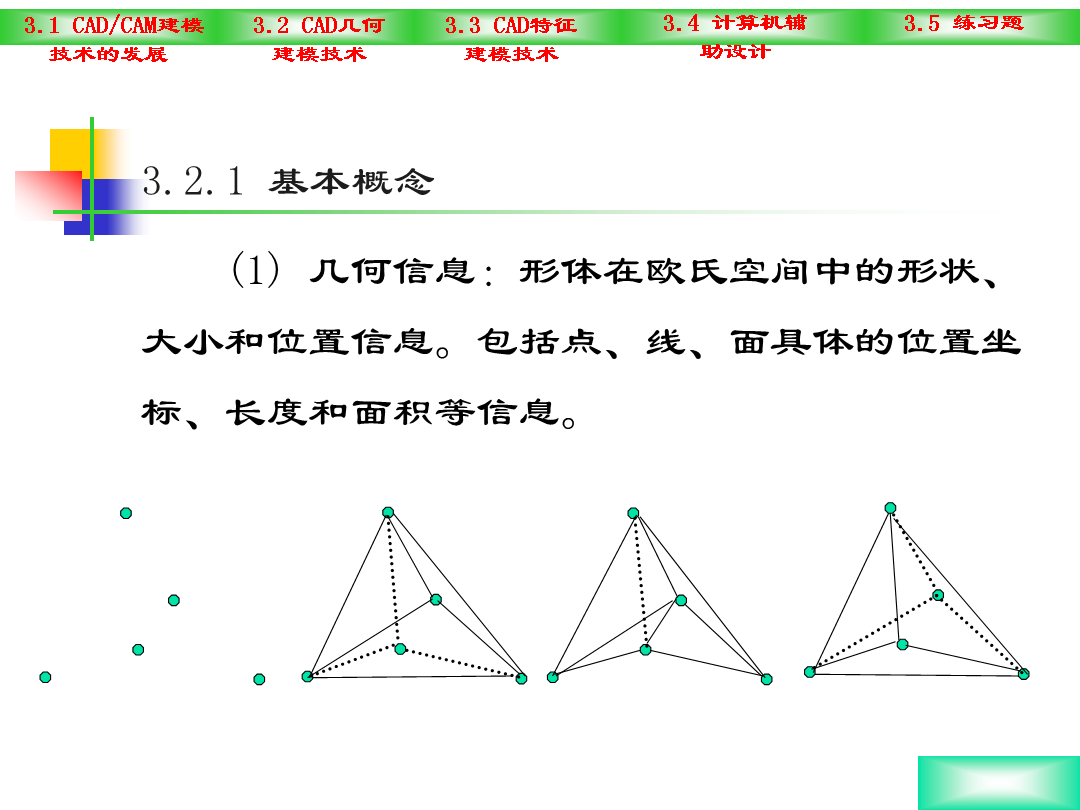
第五章机械(jīxiè)CAD/CAM建模技术5.1几何(jǐhé)建摸概述CAD/CAM几何建模基本知识几何信息(xìnxī):是指形体的形状、位置和大小的信息(xìnxī)。如:直线描述方程,矩形体的长宽高等。拓扑信息(xìnxī):反映形体各组成元素数量及其相互间关系。如:相交、相邻、相切、垂直、平行等。注意:两形体几何信息(xìnxī)相同,若拓扑信息(xìnxī)不同,则两形体可能完全不同。形体基本元素:点、边、面形体(xíngtǐ)六层拓朴结构正则集与正则集合运算正则集:一集合S的内部闭包与原

CADCAM建模技术及应用.pptx
3.1模型的基本概念线框模型线框建模(wireframemodel)线框模型的特点表面建模(surfacemodel)表面建模的过程表面模型的特点实体建模(solidmodel)线框模型和表面模型在完整、准确地表达实体形状方面各有其局限性,要想完整地处理三维立体的各种问题,就必须采用实体模型。实体模型是在表面模型的基础上,再定义物体存在于面的哪一侧而建立的。实体模型在定义表面的同时还定义了该表面的外法矢方向。实体模型的数据结构较复杂实体模型与线框模型和表面模型的根本区别在于:不但记录了全部几何信息,而且记

第4章机械CADCAM建模技术.ppt
几何建模过程CAD/CAM技术多面体拓扑元素的拓扑关系描述方式(9种)CAD/CAM技术CAD/CAM技术与表面模型的区别边界表示法的表面必须封闭、有向,各张表面间有严格的拓扑关系,形成一个整体;而表面模型的面可以不封闭,面的上下表面都可以有效,不能判定面的哪一侧是体内与体外;此外,表面模型没有提供各张表面之间相互连接的信息。CAD/CAM技术特征的含义:a.特征不是体素,是某个或某几个加工表面;b.特征不是完整的零件;c.特征的分类与该表面的加工工艺规程密切相关;d.特征信息包括几何信息及约束信息外,还
