
伪随机序列的设计与分析.doc

Ja****20


在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

伪随机序列的设计与分析.doc
伪随机序列的设计与分析随着通信和信息技术的发展,二元伪随机序列在通信学,密码学,雷达测距等方面都得到了广泛的应用.故而也带动了对伪随机序列的研究兴趣.本文的研究内容主要包含以下三个方面:伪随机序列集的设计,伪随机序列的2-adic复杂度和线性复杂度,以及环上序列的压缩映射.本文得到的结果可概括如下(一)在序列集的设计方面,本文构造了一类低相关区域序列集和一类低相关值序列集.(1)设计低相关区域序列集的方法主要是通过修改理想两值自相关序列的部分比特来获得新的序列.而且新构造的低相关区域序列集能达到Tang-

伪随机序列码的性能分析毕业(论文)设计.doc
题目伪随机序列码的性能分析学生姓名薛康学号1113024126所在学院物理与电信工程学院专业班级通信工程专业1104班指导教师魏瑞__完成地点物理与电信工程学院实验室2015年5月25日毕业论文﹙设计﹚任务书院(系)物电学院专业班级通信1104班学生姓名薛康一、毕业论文﹙设计﹚题目伪随机序列码的性能分析二、毕业论文﹙设计﹚工作自__2015_年_1_月_1_日起至_2015_年6月__10_日止三、毕业论文﹙设计﹚进行地点:物电学院北区实验室四、毕业论文﹙设计﹚的内容要求:扩频序列的设计和选择是扩频通信的

伪随机序列的设计与分析研究的综述报告.docx
伪随机序列的设计与分析研究的综述报告随机序列在信息传输、数据加密等领域发挥着重要作用,但在某些应用场景下,我们需要一种可预测、可重复的序列,这时伪随机序列就应运而生。本文将对伪随机序列的设计与分析进行综述。1.什么是伪随机序列?伪随机序列是一种类似随机序列的序列,在外观和统计上与随机序列相似,但其产生过程有规则可循且可预测,且长度一般为有限的序列。伪随机序列的应用非常广泛,例如:用于密码学中秘钥的生成、模拟通信过程、生成模拟信号、让计算机在游戏中感觉到随机性等。2.伪随机序列的设计如何设计一种高质量的伪随

伪随机序列的毕业(设计)论文.doc
摘要本毕业设计主要介绍了两种常用的反馈移位寄存器序列(m序列和Gold序列)的特性,并对其进行仿真研究。伪随机序列良好的随机性和接近于白噪声的相关函数,使其易于从信号或干扰中分离出来。伪随机序列的可确定性和可重复性,使其易于实现相关接收或匹配接收,因此有良好的抗干扰性能。伪随机序列的这些特性使得它在伪码测距、导航、遥控遥测、扩频通信、多址通信、分离多径、数据加扰、信号同步、误码测试、线性系统、各种噪声源等方面得到了广泛的应用,特别是作为扩频码在CDMA系统中的应用已成为其中的关键问题。在本论文中首先简要阐
伪随机序列.ppt
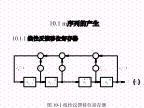
10.1m序列的产生由于带有反馈,因此在移位脉冲作用下,移位寄存器各级的状态将不断变化,通常移位寄存器的最后一级做输出,输出序列为1.线性反馈移位寄存器的递推关系式递推关系式又称为反馈逻辑函数或递推方程。设图10-1所示的线性反馈移位寄存器的初始状态为(a0a1…an-2an-1),经一次移位线性反馈,移位寄存器左端第一级的输入为2.线性反馈移位寄存器的特征多项式用多项式f(x)来描述线性反馈移位寄存器的反馈连接状态:10.1.2m序列产生器图10-2m序列产生器10.2.1均衡特性(平衡性)10.2
