
有限单元法原理及应用.ppt

和蔼****娘子









亲,该文档总共339页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

有限单元法原理及应用.ppt
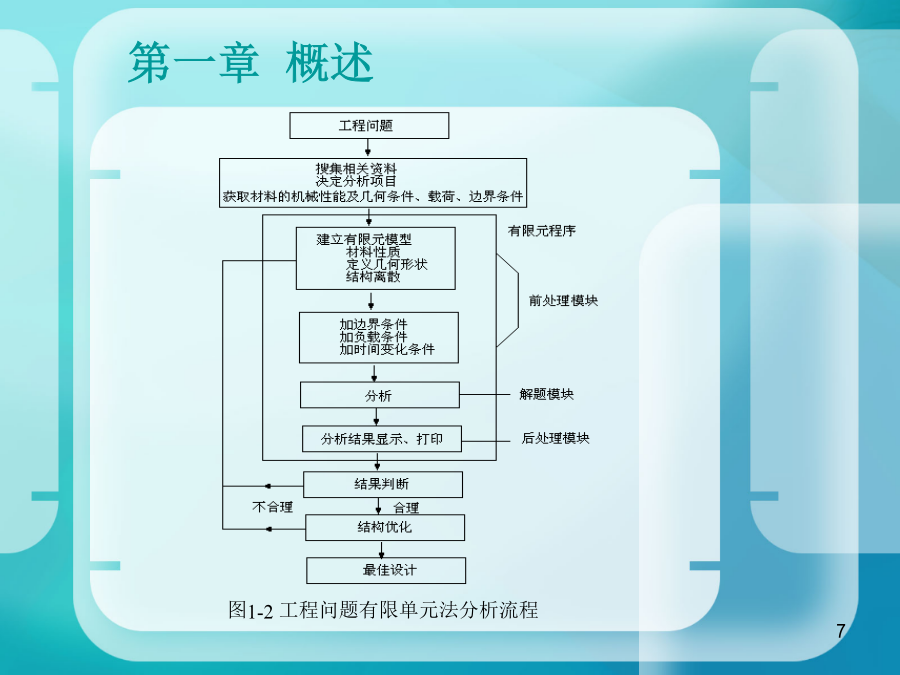
感谢大学力学论坛网友分享有限单元法原理及应用简明教程内容结构第一章概述第一章概述1.2有限单元法基本步骤图1-2工程问题有限单元法分析流程1.3工程实例第一章概述第一章概述第二章结构几何构造分析2.1结构几何构造的必要性(a)结构本身可变(b)缺少必要的约束条件(c)约束汇交于一点图2-1几何可变结构2.2结构计算基本知识2.2.2结构的分类与基本特征(3)按结构自由度分①静定结构——自由度为零的几何不变结构。其特征:a.静定结构的内力及支座反力可全部由平衡方程式求出,并且解答是唯一的。b.静定结构的内力

有限单元法原理及应用.ppt
感谢大学力学论坛网友分享有限单元法原理及应用简明教程内容结构第一章概述第一章概述1.2有限单元法基本步骤图1-2工程问题有限单元法分析流程1.3工程实例第一章概述第一章概述第二章结构几何构造分析2.1结构几何构造的必要性(a)结构本身可变(b)缺少必要的约束条件(c)约束汇交于一点图2-1几何可变结构2.2结构计算基本知识2.2.2结构的分类与基本特征(3)按结构自由度分①静定结构——自由度为零的几何不变结构。其特征:a.静定结构的内力及支座反力可全部由平衡方程式求出,并且解答是唯一的。b.静定结构的内力

有限单元法原理与应用.ppt
有限单元法原理与应用2.1连续介质的离散化连续介质的有限单元分析包含三个基本方面:介质的离散化、单元特性计算以及单元组合体的结构分析。2.2位移函数因此可以得到:为了简化位移函数的表达式,记:2.3单元应变2.4初应变对于平面应变问题对于层状各项异性材料:2.5平面应力由以上可以解出:或应力矩阵2.各项同性体——平面应变其中:3.各向异性体平面应力问题的弹性矩阵为:当层面与x轴有一倾角时[D]必须进行变换。则在(x’,y’)中,

有限单元法原理及应用简明教程.ppt
有限单元法原理及应用简明教程内容结构第一章概述第一章概述1.2有限单元法基本步骤图1-2工程问题有限单元法分析流程1.3工程实例第一章概述第一章概述第二章结构几何构造分析2.1结构几何构造的必要性(a)结构本身可变(b)缺少必要的约束条件(c)约束汇交于一点图2-1几何可变结构2.2结构计算基本知识2.2.2结构的分类与基本特征(3)按结构自由度分①静定结构——自由度为零的几何不变结构。其特征:a.静定结构的内力及支座反力可全部由平衡方程式求出,并且解答是唯一的。b.静定结构的内力及支座反力与材料的性质和

塑性有限单元法应用.pptx
塑性有限(yǒuxiàn)单元法应用宏观(hóngguān)尺度材料设计有限元方法宏观(hóngguān)尺度材料设计有限元方法宏观尺度(chǐdù)材料设计有限元方法宏观尺度材料设计(shèjì)有限元方法宏观尺度材料设计(shèjì)有限元方法宏观(hóngguān)尺度材料设计有限元方法宏观(hóngguān)尺度材料设计有限元方法宏观尺度材料(cáiliào)设计有限元方法宏观尺度材料(cáiliào)设计有限元方法宏观尺度材料设计(shèjì)有限元方法宏
