《2016高考文数预测密卷》新课标I卷 Word版含解析.doc

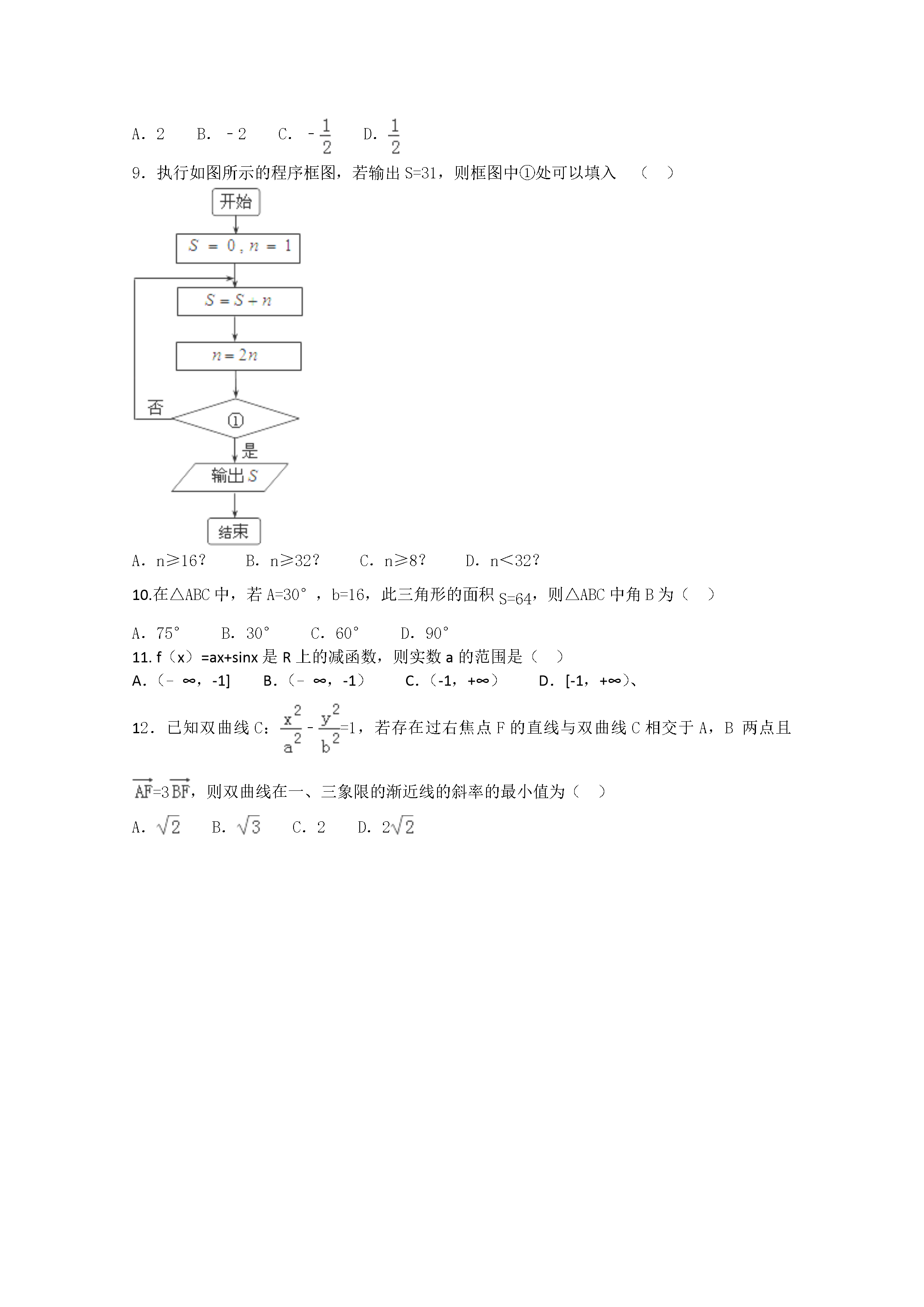
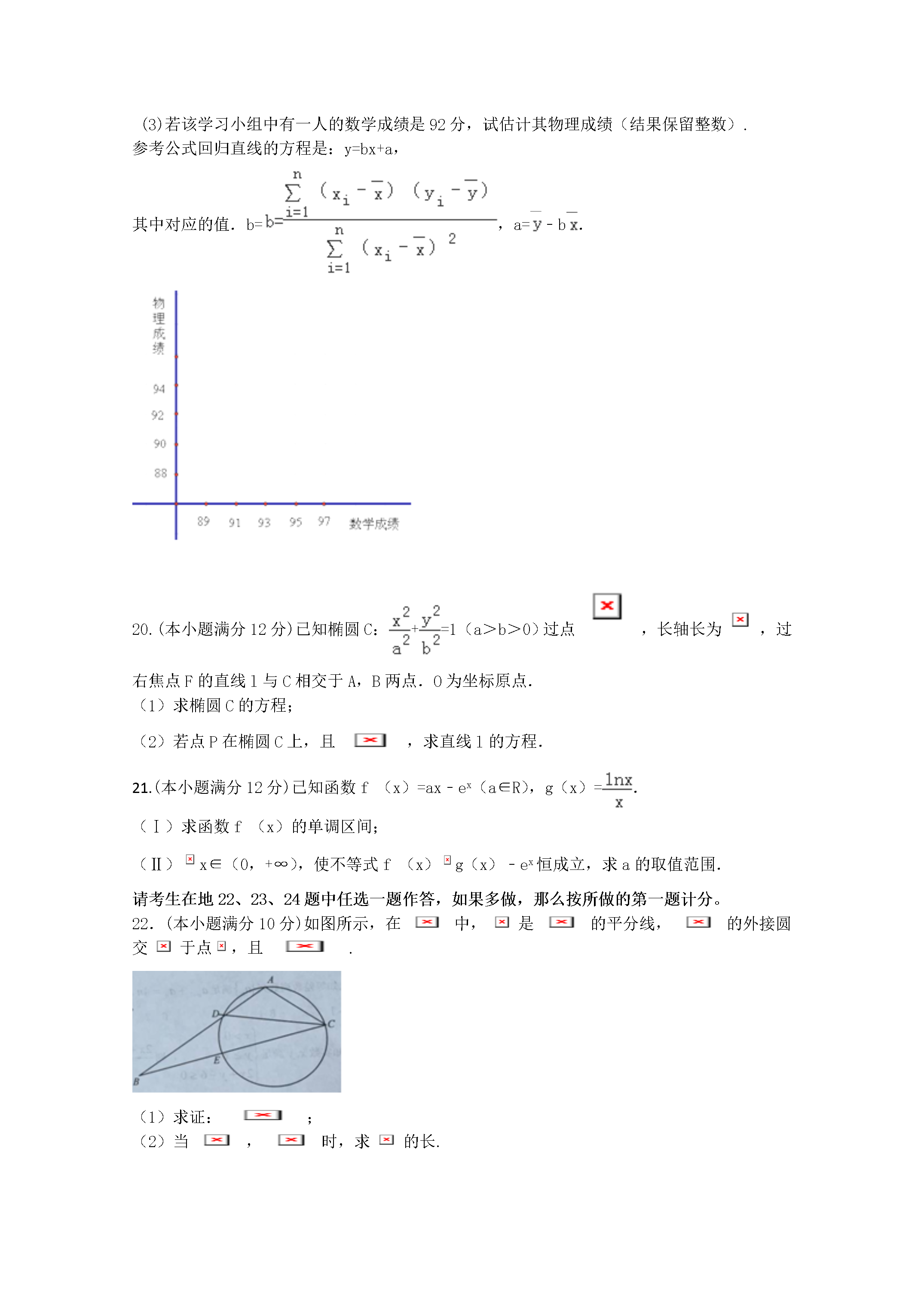
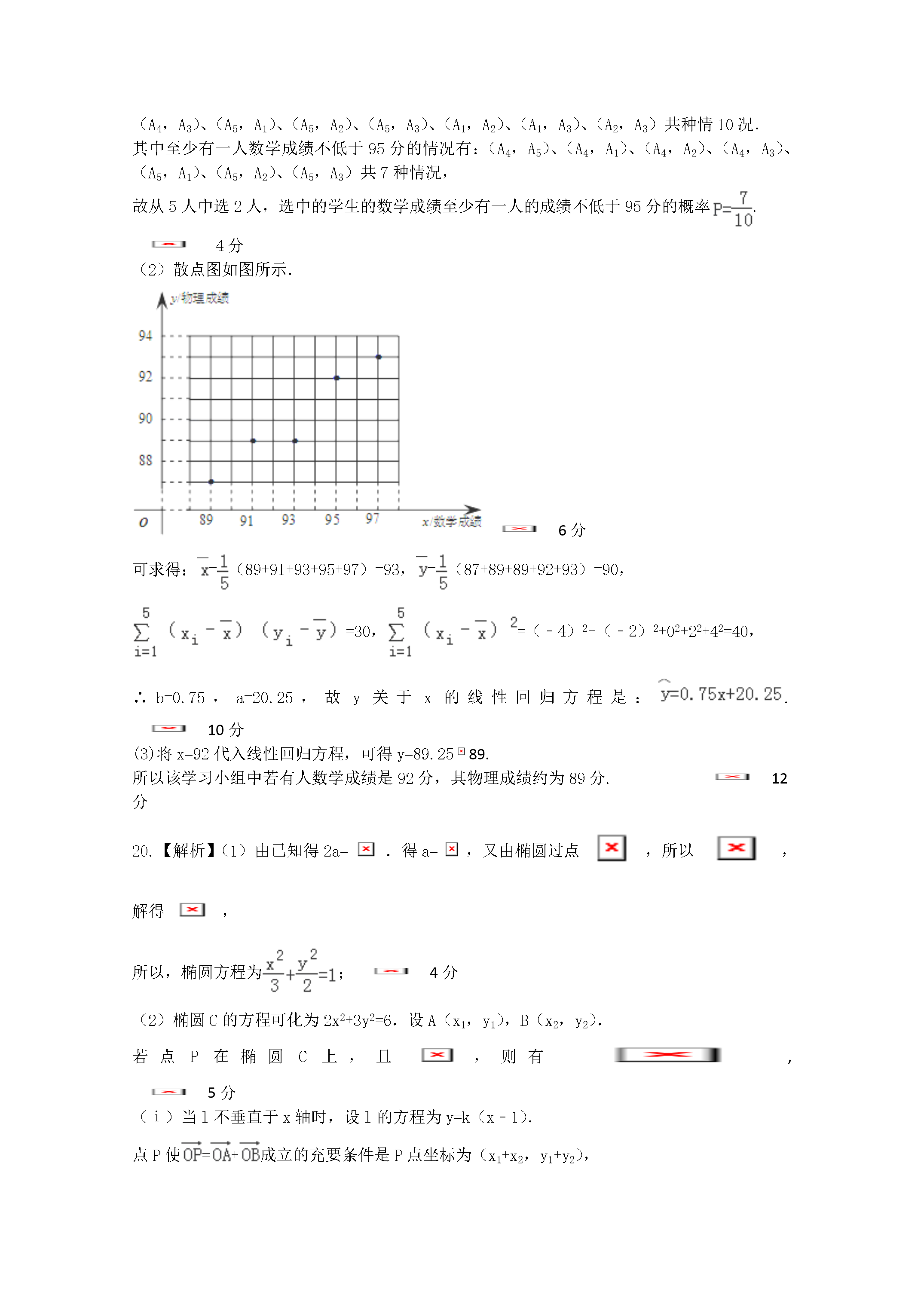
《2016高考文数预测卷》新课标I卷一、选择题（本大题共12小题，每小题5分，共60分，在每个小题给出的四个选项中，只有一项是符合题目要求的）1．已知复数z=1﹣i，则的虚部是（）A．0B．2C．-2iD．﹣22．“a=2”是“直线l1：（a+2）x+（a﹣2）y=1与直线l2：（a﹣2）x+（3a﹣4）y=2相互垂直”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件3．抛物线的焦点坐标为()A.(0,2)B.(-2,0)C.(2,0)D.(0,-2)4．已知函数，使函数值为17的x的值是（）A．B．或C．D．5．将函数y=sin2x的图象向右平移个单位，再将图象上各点的横坐标伸长到原来的2倍，纵坐标不变，则所得图象对应的函数解析式是（）A．y=-cos4xB．y=-cosxC．y=sin（x+）D．y=-sinx6．下列各式中最小值为2的是（）A．B．C．D．7．某几何体的三视图如图所示，则该几何体的表面积等于（）A．B．C．D．38．设曲线y=在点（2，3）处的切线与直线ax+y+1=0垂直，则a=（）A．2B．﹣2C．﹣D．9．执行如图所示的程序框图，若输出S=31，则框图中①处可以填入（）A．n≥16？B．n≥32？C．n≥8？D．n＜32？10.在△ABC中，若A=30°，b=16，此三角形的面积S=64，则△ABC中角B为（）A．75°B．30°C．60°D．90°11.f（x）=ax+sinx是R上的减函数，则实数a的范围是（）A．（﹣∞，-1]B．（﹣∞，-1）C．（-1，+∞）D．[-1，+∞）、12．已知双曲线C：﹣=1，若存在过右焦点F的直线与双曲线C相交于A，B两点且=3，则双曲线在一、三象限的渐近线的斜率的最小值为（）A．B．C．2D．2第II卷（非选择题共90分）二、填空题（本大题共4个小题，每小题5分，共20分）13.设Sn为数列{an}的前n项和，若Sn=8an﹣1，则=.14．设x，y满足，则的最小值为.15.已知中，，点在平面内，且，则的最小值为．16.如果椭圆的某条弦被点（2,4）平分,则这条弦所在的直线方程是_________（请写出一般式方程）三、解答题（本大题共6个小题，共70分，解答应写出必要的文字说明、证明过程或演算步骤）17.(本小题满分12分)已知数列{an}的前n项和Sn=n，（1）求通项公式an的表达式；（2）若，求数列{bn}的前n项和Tn．18．(本小题满分12分)如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形．∠DAB=60°，AB=2AD，PD⊥底面ABCD．（Ⅰ）证明：PA⊥BD（Ⅱ）设PD=AD=1，若M是PB的中点，求棱锥M﹣ABC的体积．19.(本小题满分12分)在一次考试中，某班学习小组的五名学生的数学、物理成绩如下表（1）要在这五名学生中选2名参加一项活动，求选中的同学中至少有一人的数学成绩不低于95分的概率．（2）请在所给的直角坐标系中画出它们的散点图，并求出这些数据的线性回归直线方程.(3)若该学习小组中有一人的数学成绩是92分，试估计其物理成绩（结果保留整数）.参考公式回归直线的方程是：y=bx+a，其中对应的值．b=，a=﹣b．20.(本小题满分12分)已知椭圆C：+=1（a＞b＞0）过点，长轴长为，过右焦点F的直线l与C相交于A，B两点．O为坐标原点．（1）求椭圆C的方程；（2）若点P在椭圆C上，且，求直线l的方程．21.(本小题满分12分)已知函数f（x）=ax﹣ex（a∈R），g（x）=．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）x∈（0，+∞），使不等式f（x）g（x）﹣ex恒成立，求a的取值范围．请考生在地22、23、24题中任选一题作答，如果多做，那么按所做的第一题计分。22．(本小题满分10分)如图所示，在中，是的平分线，的外接圆交于点，且.（1）求证：；（2）当，时，求的长.23.(本小题满分10分)在平面直角坐标系xOy中，圆C的参数方程为（θ为参数），直线l经过点P（1，1），倾斜角，（1）若以直角坐标原点为极点，x轴的正半轴为极轴，建立极坐标系，写出直线l的极坐标方程与参数方程；（2）设l与圆C相交于两点A，B，求点P到A，B两点的距离之和．24.(本小题满分10分)设函数.（1）若，解不等式；（2）若函数有最小值，求实数的取值范围.《2016高考文数预测卷》新课标I卷参考答案1.D【解析】∵z=1﹣i，∴=．所以虚部是-2，故选D．2．A【解析】当a=2时，两条直线分别化为：4x=1，y=1，此时两条直线相互垂直；当a=时，两条直线分别化为：10x﹣2y=3，x=﹣3，此时两条直线不相互垂直，舍去；当a≠，2时，由两条直线相互垂直，∴﹣×=﹣1，解得a=．综上可