
3.doc

静芙****可爱



在线预览结束,喜欢就下载吧,查找使用更方便
相关资料
学案-全国-2010_七年级信息技术 在因特网上浏览信息(学案)全国通用.rar
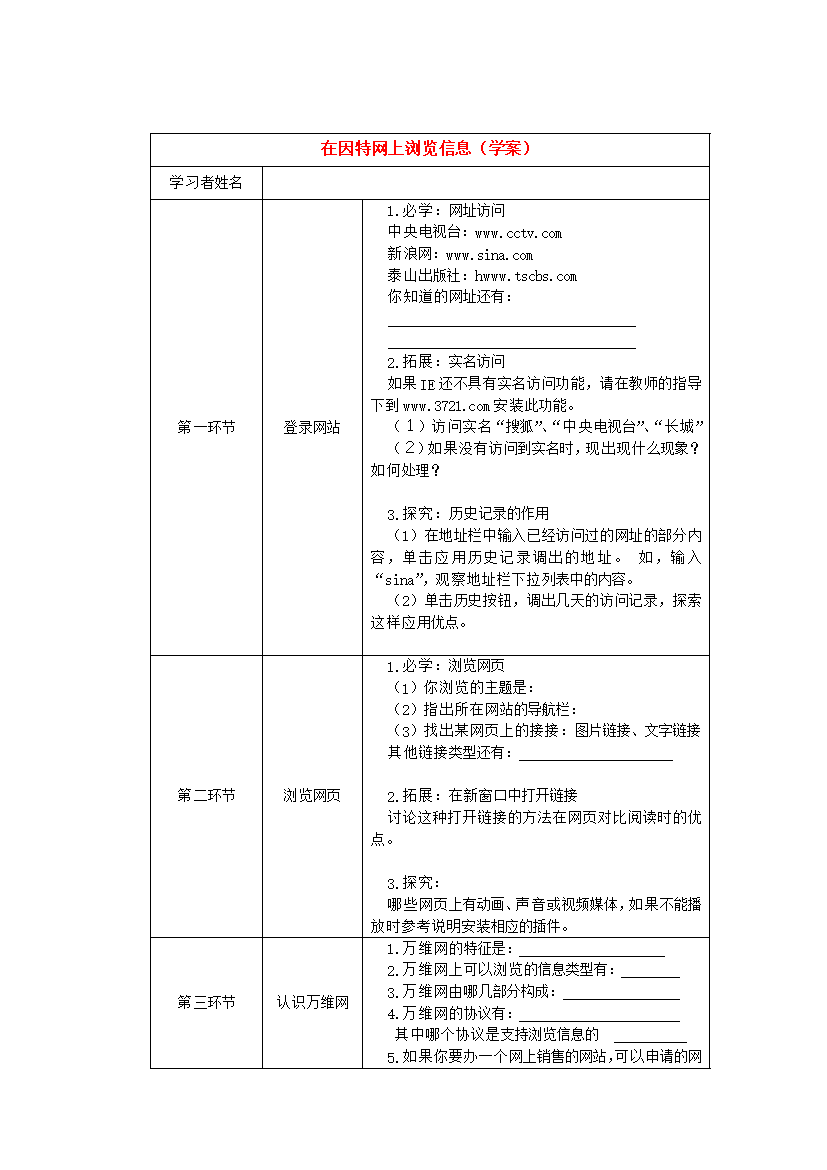
在因特网上浏览信息(学案)学习者姓名第一环节登录网站1.必学:网址访问中央电视台:www.cctv.com新浪网:www.sina.com泰山出版社:hwww.tscbs.com你知道的网址还有:2.拓展:实名访问如果IE还不具有实名访问功能,请在教师的指导下到www.3721.com安装此功能。(1)访问实名“搜狐”、“中央电视台”、“长城”(2)如果没有访问到实名时,现出现什么现象?如何处理?3.探究:历史记录的作用(1)在地址栏中输入已经访问过的网址的部分内容,单击应用历

3-3-3.ppt
考点三补写句子补写句子表面是对语言表达连贯能力的考查,实际上是对考生综合语言表达能力的考查。这类题目一般要求“根据材料内容”补写句子。因此,所补写的句子的内容、语言要从上下文的有关材料中去提炼和概括,离开文本不可能补写正确。要准确地补写句子就要把握补写句子的步骤和几类句子的补写方法。一、补写句子的步骤解答时要结合具体语境分析,按步骤答题:第一步:审题干,明要求。做题之前一定要认真审题,如“语意完整连贯,内容贴切,逻辑严密。每处不超过10个字”等,尤其要注意字数限制。第二步:读语段,通大意。语句补写题虽说考

3-3-3.ppt
考点三补写句子补写句子表面是对语言表达连贯能力的考查实际上是对考生综合语言表达能力的考查。这类题目一般要求“根据材料内容”补写句子。因此所补写的句子的内容、语言要从上下文的有关材料中去提炼和概括离开文本不可能补写正确。要准确地补写句子就要把握补写句子的步骤和几类句子的补写方法。一、补写句子的步骤解答时要结合具体语境分析按步骤答题:第一步:审题干明要求。做题之前一定要认真审题如“语意完整连贯内容贴切逻辑严密。每处不超过10个字”等尤其要注意字数限制。第二步:读语段通大意。语句补写题虽说考的主要是语

m3u3lh3-3.ppt
MarkTwainTheMillionPoundBank-NoteHenryisrescuedatseabyaBritishshipthattakeshimtoLondonwherehefoundhimselfwithoutmoney.Hungryandalonehewalksthestreetsofthecityhopingtofindajob.TworichbrothersRoderickandOliverhavemad

m3u3lh3-3.ppt
MarkTwainTheMillionPoundBank-NoteHenryisrescuedatseabyaBritishshipthattakeshimtoLondonwherehefoundhimselfwithoutmoney.Hungryandalone,hewalksthestreetsofthecityhopingtofindajob.Tworichbrothers,RoderickandOliver,havemadeasecretbet.Roderickbelievesthatamanca
