方差分析及回归分析.ppt

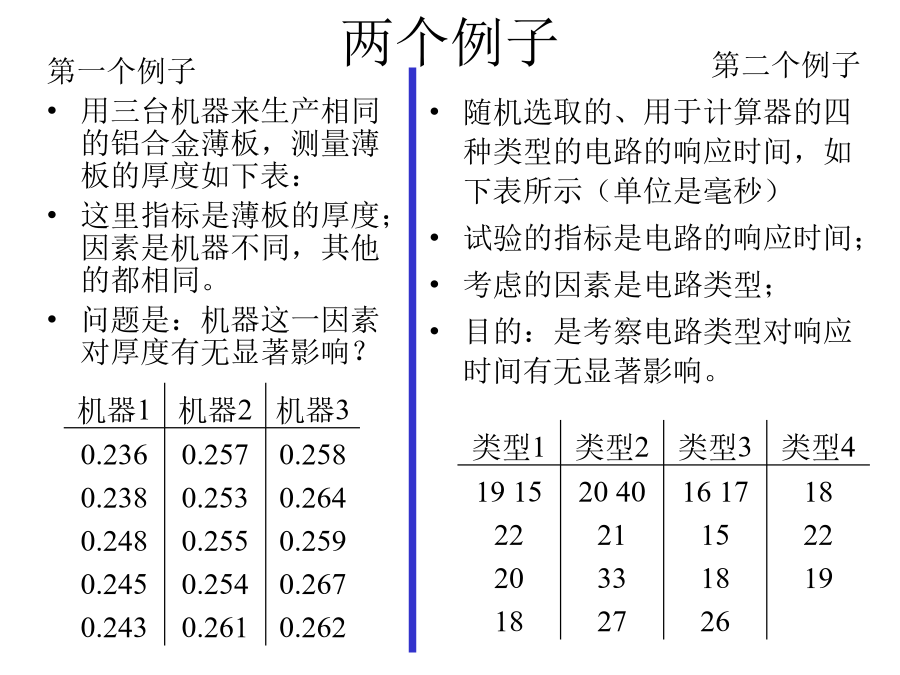
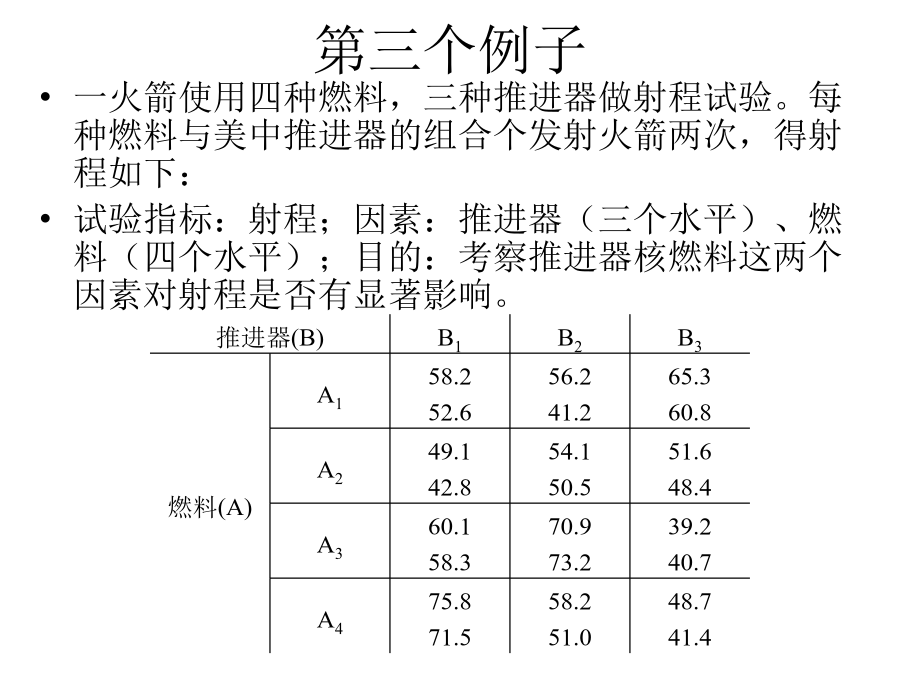
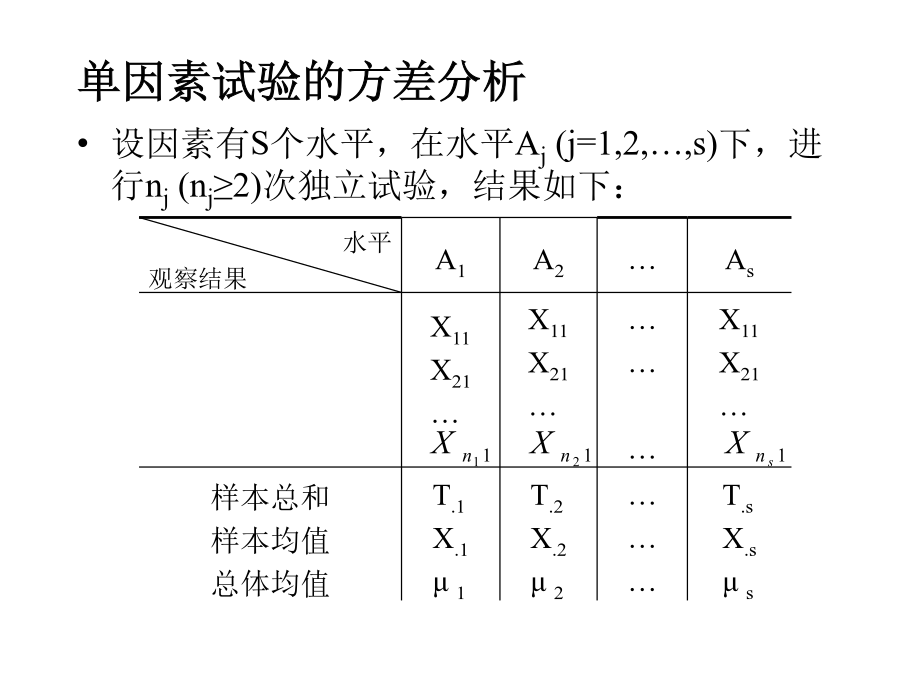
第九章、方差分析及回归分析§1单因素试验的方差分析化学生产中，因素有：原料成分、原料剂量、催化剂、反应温度、压力、反应时间、机器设备、操作人员水平等。
目的：决定各种因素，使生产过程得以稳定。
方法：先进行试验。
试验的分析：利用方差分析来分析试验的结果。
根据影响试验结果的因素的多少分为单因素试验的方差分析和多因素试验的方差分析。两个例子第三个例子问题的讨论--（单因素试验）单因素试验的方差分析假定，各个水平Aj(j=1,2,…,s)下样本X1j，X2j，…，
来自具有相同方差σ2，均值分别为μj(j=1,2…s)的正态总体，μj和σ2未知且在不同水平Aj下的样本之间相互独立。方差分析的任务

而假设（1.2)等价于假设

我们来导出上述假设检验的检验统计量。(二）平方和的分解上式的第三项为SE称为误差平方和，SA表示Aj水平下的样本均值与数据总平均的差异，叫做效应平方和，他是由水平Aj的效应的差异以及随机误差引起的。（三）SE，SA的统计特性1、SE的统计特性可以计算
这里
2、SA的统计特性，它是s个变量
的平方和，且仅有一个线性约束条件:

因此的知SA的自由度是s-1。
（由（1，3），（1，6）及Xij的独立性得知
经计算可以证明SE，SA的是相互独立的，且H0当为真时

（四）假设检验问题的拒绝域
由（1，15）式，当H0为真时

所以SA/(s-1)是σ2的无偏估计,而当当H1为真时，

这时
而由于由于

所以检验问题(1，2)’的拒绝域的形式是：

其中k由预先给定的显著性水平α确定，由此得此检验问题的拒绝域是：

因此，可以得到单因素方差分析表如下页单因素试验的方差分析表（1，21）判断：因为Fα(2,12)=3.89<32.92，故在水平0.05下拒绝H0，即认为各台机器生产的薄板厚度有显著差异。（五）未知参数的估计具体做法是
由于
于是

因此均值差μj-μk=δj-δk的置信水平为1-α的置信区间是例5求例4中的未知参数σ2，μj，δj的点估计及均值差的置信水平为0.95的置信区间。
解：经计算

由t0.025(n-s)=t0.025(12)=2.1788，得

故μ1–μ2，μ1–μ3，μ2–μ3的置信水平为0.95的置信区间分别为例6设在第二个例子中，四类电路的响应时间的总体均为正态分布，切割总体的方差相同，但参数未知，并且个样本相互独立。取水平α=0.05，检验各类电路的响应时间是否有显著差异。解以μ1，μ2，μ3，μ4，记类型ⅰ，ⅱ，ⅲ，ⅳ四种电路的响应时间总体平均值。我们需要检验：
H0：μ1=μ2=μ3=μ4，
H1：μ1，μ2，μ3，μ4不全相等
由于n=18,s=4,n1=n2=n3=5,n4=3，因为F0.05(3,14)=3.34<3.76，故在水平0.05下拒绝H0，认为各类型电路的响应时间有显著差异。#一元线性回归第三节、一元线性回归回归分析的任务例1为研究某一化学反应过程中温度(x,)与产品得率y的影响。得数据如下表：

其散点图如右
从图中可以看出
它是一条直线，
因此μ(x)具有形式
μ(x)=a+bx设Y关于x的回归函数为μ(x)。利用样本来估计μ(x)的问题称为求Y关于x的回归问题。
若μ(x)是线性函数μ(x)=a+bx，此时的估计问题称为求一元线性回归问题。
一元线性回归模型：
设Y~N(a+bx,σ2)其中a,b,σ2是未知参数，记
ε=Y-（a+bx），则
Y=a+bx+ε,ε~N(0,σ2)（1）
称上式为一元线性回归模型。
称a+bx为x的线性函数，而ε~N(0,σ2)是随机误差。二、a、b的估计则变为求Q(a,b)的最小值。
令

得方程组：

称这个方程组为正规方程组。正规方程组的系数行列式为

故正规方程组有唯一一组解
这时我们把作为回归函数μ(x)=ax+b的估计。称为Y关于x的经验回归函数。
称方程为经验回归方程，简称回归方程。
也可以把经验回归方程写为
若记
这时，a,b的估计值是

在例1中，测得温度对产品得率的关系是

为了求回归方程，我们需要计算和Σ于是得回归直线方程为三、σ2的估计Qe是经验回归函数μ(x)=ax+b在xi处的函数值
与处的观察值的偏差的平方和。
我们来计算Qe根据：得Qe的分解式

计算出a,b的估计量是：若记

残差平方和服从的分布如下：

的数学期望是n-2，由此知

这就得到了σ2的无偏估计量如下页所示。x例3、在上表中求σ2的无偏估计。
根据上页的表，我们可以得到（四）线性假设的显著性检验可以证明
且可以计算

及

在H0为真时，b=0,这时
且有，即得H0的拒绝域是
几点说明：
在H0：b=0被拒绝时,认为回归效果是显著的；反之则