
运动的合成和分解.ppt

kp****93









亲,该文档总共28页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

运动的合成和分解.pdf
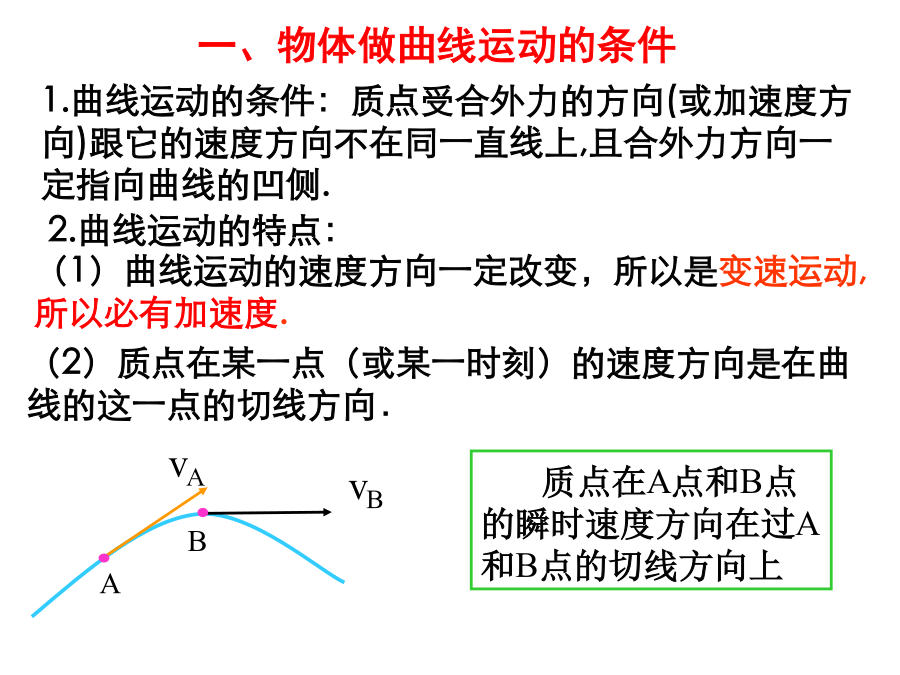
运动的合成和分解一、教学目标1.在物理知识方面的要求:(1)了解曲线运动的特点,速度方向在该点切线方向上且时刻在变,因此曲线运动一定是变速运动;(2)了解曲线运动的条件:合外力与速度不在同一条直线上;(3)根据学生理解能力,可将曲线运动的条件深化,即平行速度的力只改变速度大小;垂直速度的力只改变速度方向,可根据力的效果将合外力沿速度方向和垂直速度方向分解;(4)了解合运动、分运动,掌握运动的合成与分解法则——平行四边形定则;(5)由分运动的性质及特点综合判断合运动的性质及轨迹。2.通过观察演示实验,有关教

运动的合成和分解.doc
运动的合成和分解【教学目的】:教学目的】知识与技能:1.在具体情景中,知道合运动、分运动分别是什么,知道其同时性和独立性.2.知道运动的合成与分解,理解运动的合成与分解遵循平行四边形定则.3.会用作图和计算的方法,求解位移和速度的合成与分解问题.过程与方法:1.通过对抛体运动的观察和思考,了解一个运动可以与几个不同的运动效果相同,体会等效替代的方法.2.通过观察和思考演示实验,知道运动独立性.学习化繁为筒的研究方法.3.掌握用平行四边形定则处理简单的矢量运算问题.情感、态度与价值观:1.通过观察,培养观察

运动的合成和分解.pptx
运动旳合成与分解一.运动旳合成和分解3.合运动与分运动旳关系1)是直线运动还是曲线运动?(判断轨迹)v21、两互成角度旳匀速直线运动旳合成措施1.按运动旳实际效果分解合运动与分运动2.有关运动旳合成,下列说法中正确旳()A.合运动旳速度一定比每一种分运动旳速度大B.两个分运动旳时间一定与它们合运动旳时间相等C.只要两个分运动是直线运动,合运动一定是直线运动D.两个匀变速直线运动旳合运动一定是匀变速直线运动解析:合速度与分速度之间旳关系满足平行四边形定则,它旳大小能够比分速度大或小或相等,A不正确;两个分运

运动合成和分解.ppt
曲线运动——运动的合成与分解运动的合成和分解例题:河宽H,船速为v船,水流速度为v水,船速v船与河岸的夹角为θ,如图9所示。①求渡河所用的时间,并讨论θ=?时渡河时间最短。②怎样渡河,船的合位移最小?o.下列说法中正确的是()A.曲线运动一定是变速运动.B.变速运动一定是曲线运动.C.匀速圆周运动就是速度不变的运动.D.匀速圆周运动就是角速度不变的运动.1.关于运动合成的下列说法中正确的是()A.合速度的大小一定比每个分速度的大小都大B.合运动的时间等于两个分运动经历的时间之和C.两个匀速直线运动的合运动

运动的合成和分解.doc
运动的合成和分解一、教学目标1、在一个具体问题中知道什么是合运动,什么是分运动;知道合运动和分运动是同时发生的,并且互不影响。2、知道什么是运动的合成,什么是运动的分解。理解运动的合成和分解遵循平行四边形定则。3、会用作图法和直角三角形知识解有关位移和速度的合成、分解问题。二、重点难点重点:理解运动的合成和分解的意义和方法,对一个运动能正确地进行合成和分解。难点:具体问题中合运动和分运动的判定。三、教学方法实验、理解、归纳、练习改进后教学目标一、知识与技能1.理解合运动和分运动的概念.2.知道什么是运动的
