
余弦函数的图像与性质.docx

sy****28





在线预览结束,喜欢就下载吧,查找使用更方便
相关资料

余弦函数图像与性质.ppt
余弦函数的图象与性质定义域x-函数性质例1、求下列函数的最大值和最小值以及相应的x值:例2、判断下列函数的奇偶性:小结:探究1:函数的周期性探究2:函数的单调区间探究3:函数的值域以及函数取得最值时相应的x的值探究4:它的图像是由函数y=cosx的图像经过怎样的变换得到的?函数性质y
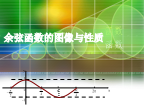
余弦函数图像与性质.ppt
-函数性质例1、求下列函数的最大值和最小值以及相应的x值:例2、判断下列函数的奇偶性:小结:探究1:函数的周期性探究2:函数的单调区间探究3:函数的值域以及函数取得最值时相应的x的值探究4:它的图像是由函数y=cosx的图像经过怎样的变换得到的?函数性质y

余弦函数的图像与性质.ppt
余弦函数的图象与性质回顾:1、正弦函数y=sinx,x∈[0,2π]的简图;x函数如何作余弦函数y=cosx(x∈R)的图象?正弦、余弦函数的图象◎五点作图法x函数y=cosx,x∈R有哪些性质?yyy余弦函数的奇偶性余弦函数的单调性y函数典例1:求下列函数的最大值和最小值以及取得最大,最小值时x的值求函数的最大最小值?以及取得最大最小值时x的值求函数的最大最小值?以及取得最大最小值时x的值典例2:判断下列函数的奇偶性:课堂练习2:判断下列函数的奇偶性求下列函数定义域:求下列函数的单调区间:比较大小小结余

余弦函数图像与性质.ppt
余弦函数的图象与性质定义域x-函数性质例1、求下列函数的最大值和最小值以及相应的x值:例2、判断下列函数的奇偶性:小结:探究1:函数的周期性探究2:函数的单调区间探究3:函数的值域以及函数取得最值时相应的x的值探究4:它的图像是由函数y=cosx的图像经过怎样的变换得到的?函数性质y

余弦函数图像与性质.ppt
编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt编辑ppt
