
高中数学 平面向量的基本定理课件 新人教A版必修4 课件.ppt

森林****来了






亲,该文档总共19页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

《平面向量的基本定理》课件(新人教A版必修4).ppt
平面向量基本定理1.向量加法的运算法则(1)力的分解M一:平面向量基本定理4、定理的价值何在?例1、已知向量,求作向量例2.例2.课堂练习知识总结:(1)平面向量基本定理;(2)向量的夹角。(3)平面向量基本定理的应用;(4)三角形中线的向量表示式;作业:莅临指导!

《平面向量的基本定理》课件(新人教A版必修4).ppt
平面向量基本定理1.向量加法的运算法则(1)力的分解M一:平面向量基本定理4、定理的价值何在?例1、已知向量,求作向量例2.例2.课堂练习知识总结:(1)平面向量基本定理;(2)向量的夹角。(3)平面向量基本定理的应用;(4)三角形中线的向量表示式;作业:莅临指导!

高中数学 平面向量的基本定理课件 新人教A版必修4.ppt
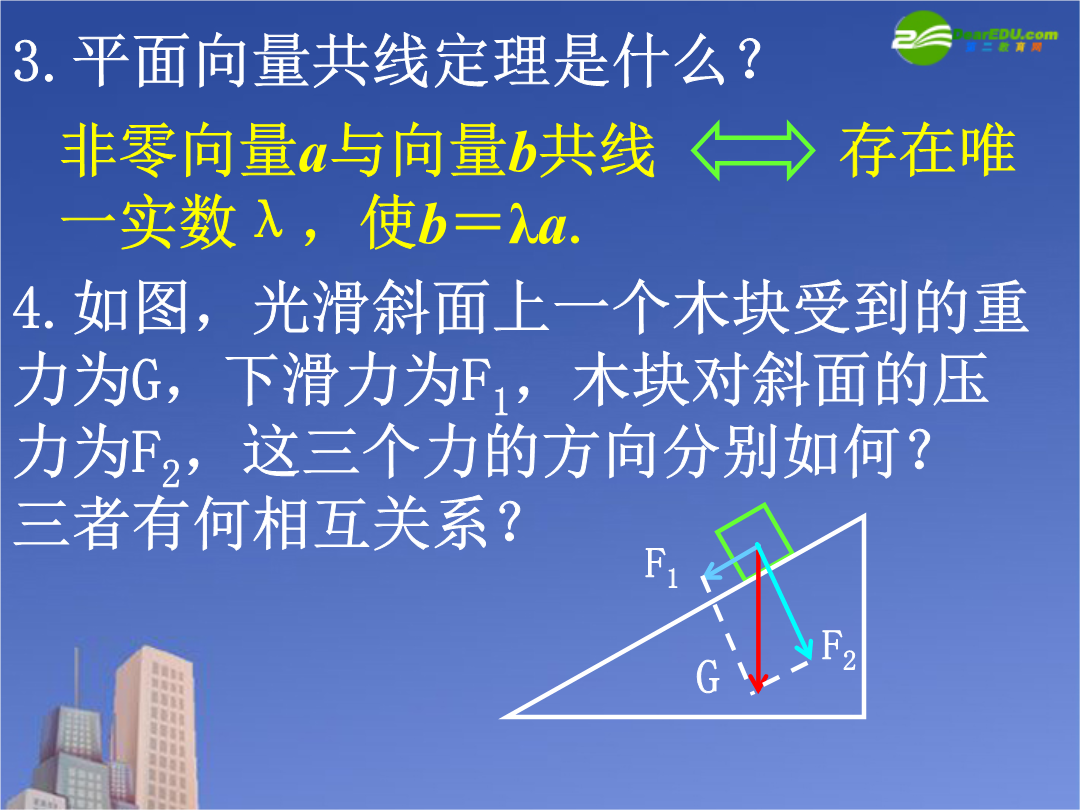
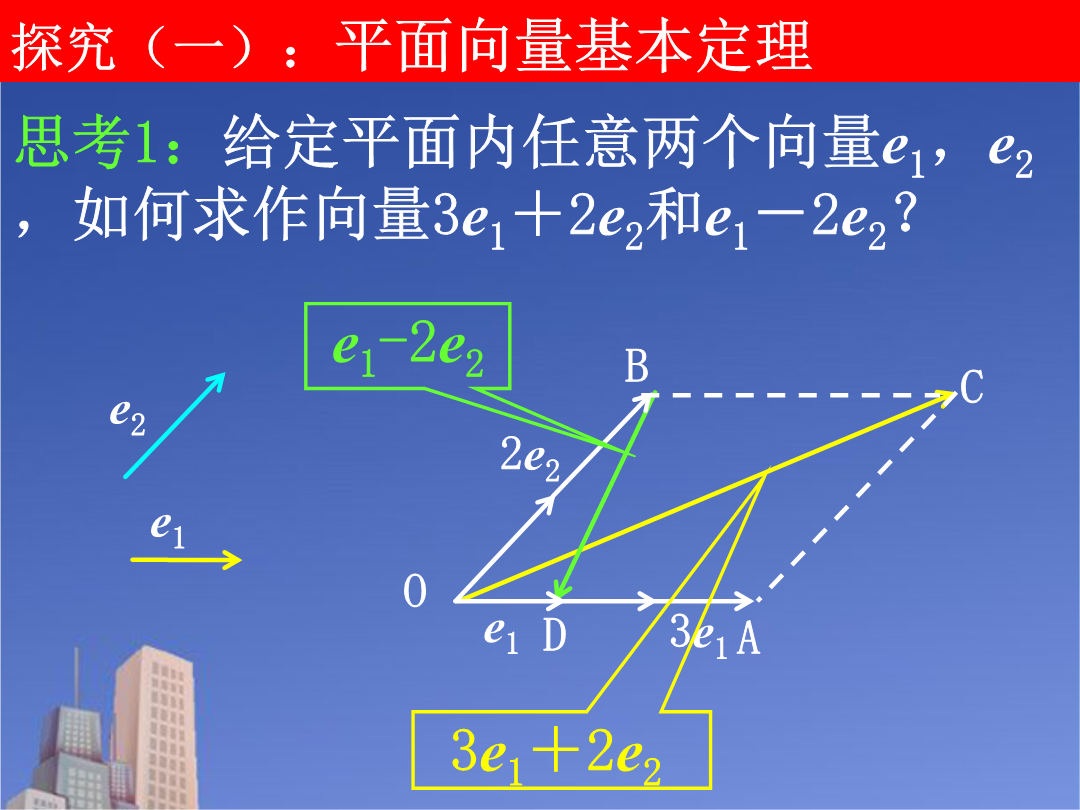
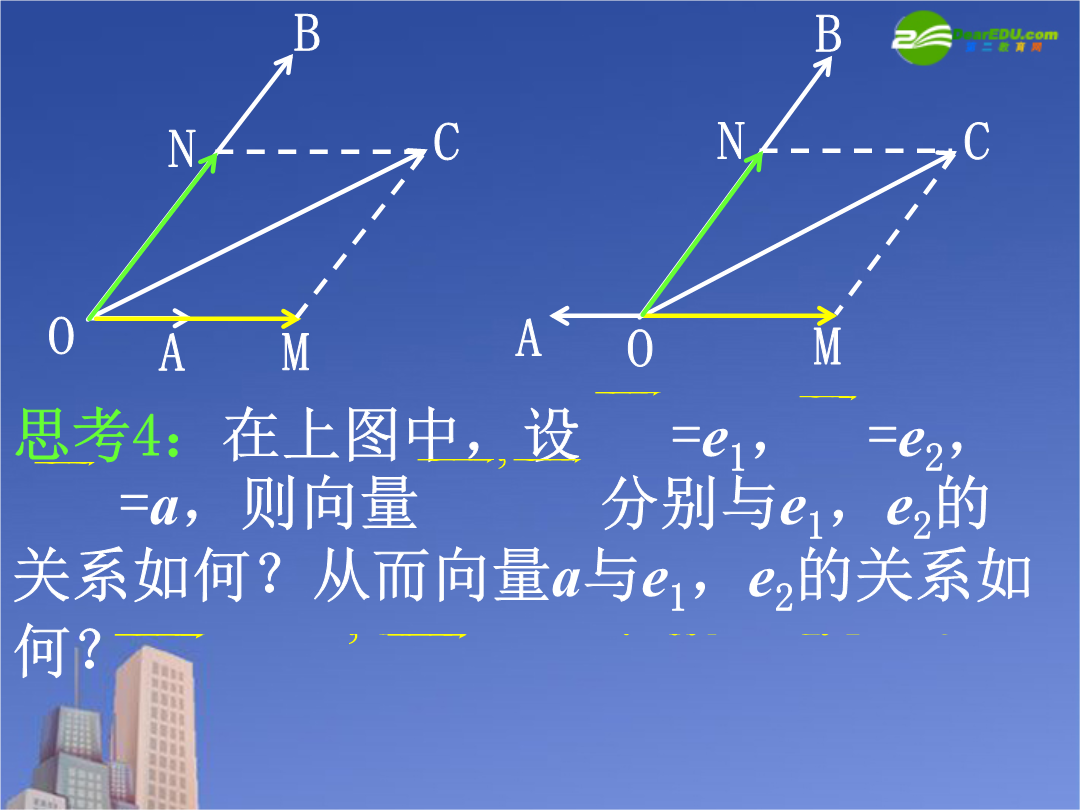
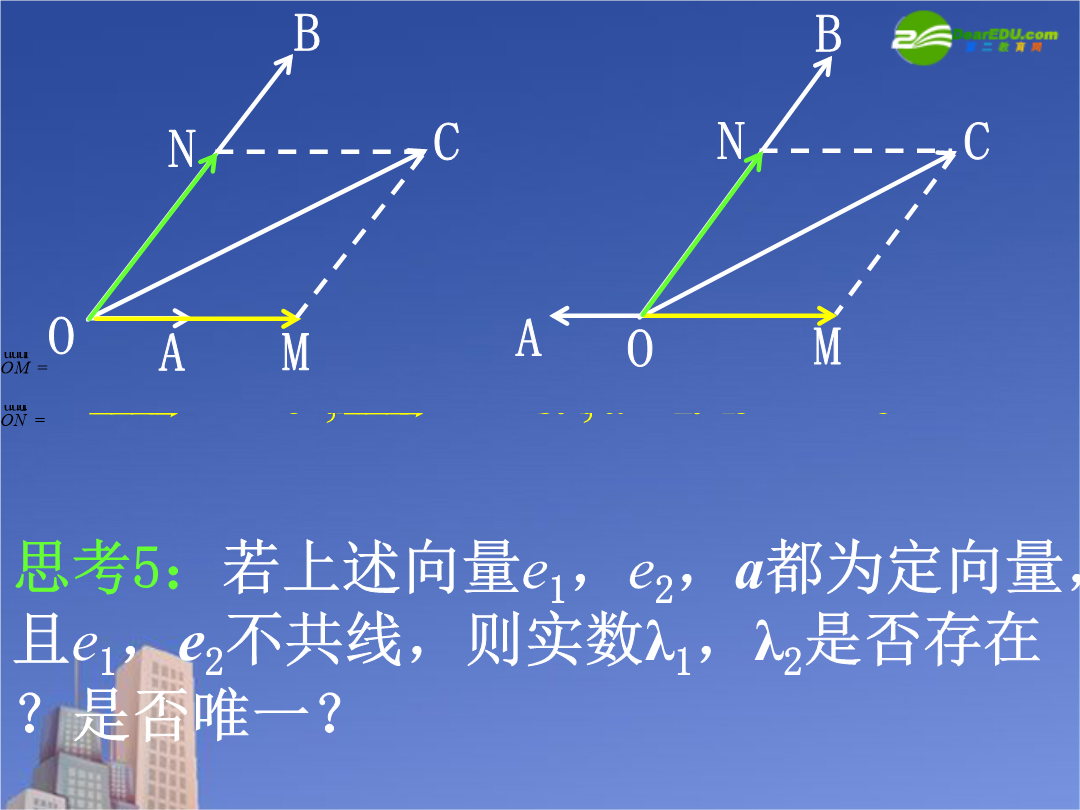
问题提出3.平面向量共线定理是什么?5.在物理中,力是一个向量,力的合成就是向量的加法运算.力也可以分解,任何一个大小不为零的力,都可以分解成两个不同方向的分力之和.将这种力的分解拓展到向量中来,就会形成一个新的数学理论.平面向量基本定理探究(一):平面向量基本定理思考2:如图,设OA,OB,OC为三条共点射线,P为OC上一点,能否在OA、OB上分别找一点M、N,使四边形OMPN为平行四边形?思考3:在下列两图中,向量不共线,能否在直线OA、OB上分别找一点M、N,使?思考4:在上图中,设=e1,=e2,

高中数学 平面向量的基本定理课件 新人教A版必修4.ppt
问题提出3.平面向量共线定理是什么?5.在物理中,力是一个向量,力的合成就是向量的加法运算.力也可以分解,任何一个大小不为零的力,都可以分解成两个不同方向的分力之和.将这种力的分解拓展到向量中来,就会形成一个新的数学理论.平面向量基本定理探究(一):平面向量基本定理思考2:如图,设OA,OB,OC为三条共点射线,P为OC上一点,能否在OA、OB上分别找一点M、N,使四边形OMPN为平行四边形?思考3:在下列两图中,向量不共线,能否在直线OA、OB上分别找一点M、N,使?思考4:在上图中,设=e1,=e2,

高中数学 平面向量基本定理课件 新人教A版必修4.rar
2.2.1平面向量基本定理问题:(1)向量a是否可以用含有e1、e2的式子来表示呢?怎样表示?a1e1+a2e2=xe1+ye2,1)平面向量基本定理的内容2)平面向量基本定理的理解3)平面向量基本定理的拓展(1)平面向量的基底有多少对?回顾小结:
