
光的衍射.doc

是你****晨呀









亲,该文档总共64页,到这已经超出免费预览范围,如果喜欢就直接下载吧~
相关资料

光的衍射及单缝衍射.ppt
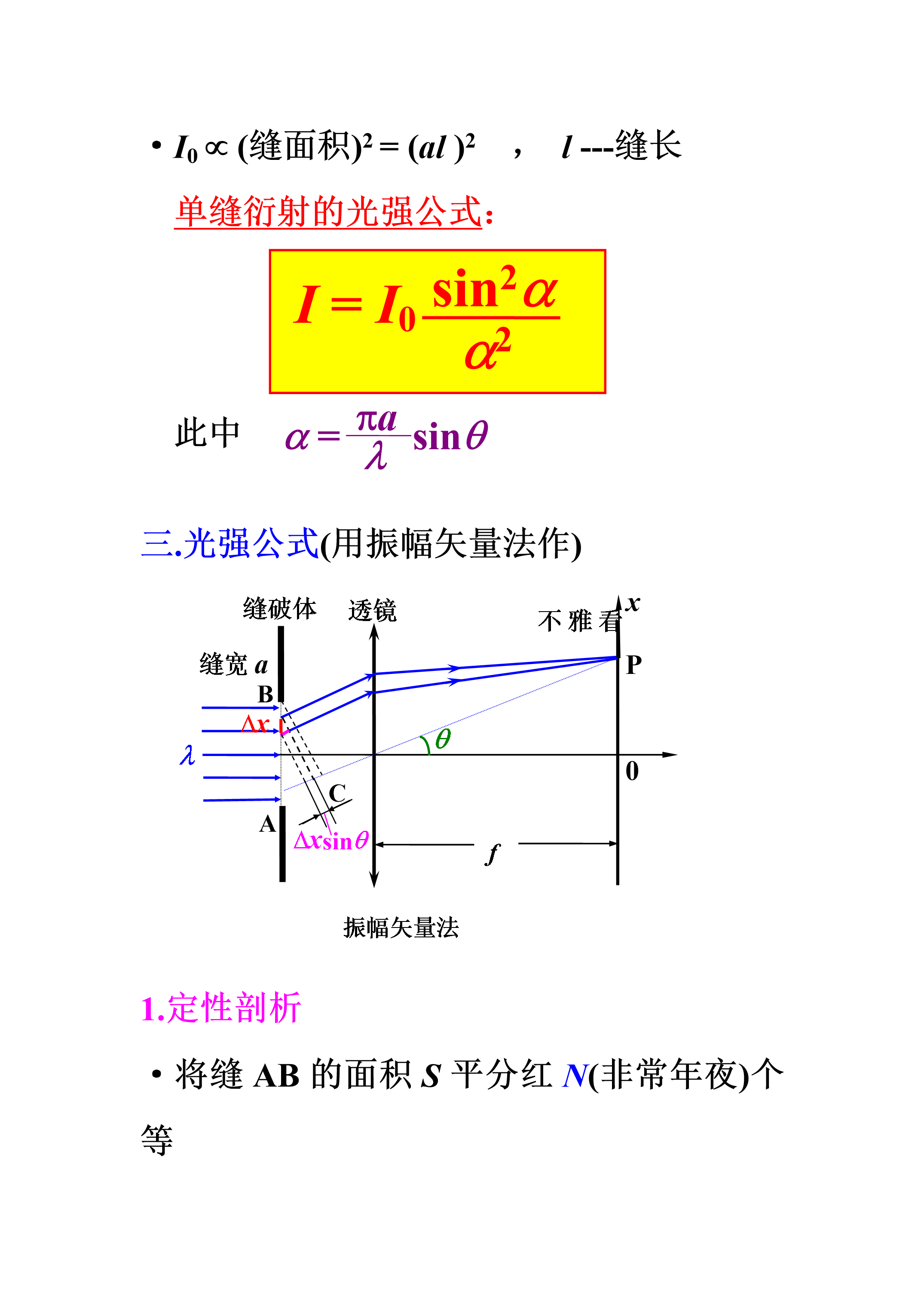
第八章光的衍射知识丰富人生科技振兴中华§8.1衍射现象、惠更斯—菲涅耳原理2、分类孔的投影刀片边缘的衍射二、惠更斯-菲涅耳原理说明菲涅耳积分可以计算任意形状波的阵面衍射问题。采用半波带法来定性地解释衍射现象。光源§8.4单缝衍射(1)单一小狭缝。(2)满足夫琅和费条件。二、菲涅耳半波带法解释单缝衍射半波带的作法:半波带λ|22.特点:将波面分成整数个波带,各波带面积相等,相邻波带的相位差为,则:暗纹中心屏幕上中央明条纹的线宽度为:(焦距f)缝宽因素(2)条纹亮度中央明纹最亮,其它明纹的光强随级次增大而迅减
光的衍射-光栅衍射.pptx
一、光栅(由于单缝衍射的影响,在应该出现干涉极大(亮纹)的地方,不再出现亮纹,称为缺级。由于单缝衍射的影响,在应该出现干涉极大(亮纹)的地方,不再出现亮纹,称为缺级。(例题2、一单色光垂直入射在光栅上,衍射光谱中共出现5条明条纹,若已知此光栅缝宽与不透明部分相等,那么在中央明纹一侧的两条明纹分别是第几级谱线?一级光谱

光的衍射.docx
光的衍射光的衍射教学目标(一)知识目标1、知道"几何光学"中所说的光沿直线传播是一种近似.?2、知道光通过狭缝和圆孔的衍射现象.?3、知道观察到明显衍射的条件(二)能力目标了解单缝衍射、小孔衍射,并能用相关知识对生活中的有关现象进行解释和分析.(三)情感目标1、让学生知道科学研究必须重视理论的指导和实践的勤奋作用;2、必须有自信心和踏实勤奋的态度;3、在学习中也要有好品质、好作风. 教学建议有关光的衍射的教学建议应该让学生了解,光的直进,是几何光学的基础,光的衍射现象并没有完全否定光的直进,而是

光的衍射_.ppt
1234578910111213141516171819202122232426272930

光的衍射.docx
光的衍射教学目标(一)知识目标1、知道"几何光学"中所说的光沿直线传播是一种近似.?2、知道光通过狭缝和圆孔的衍射现象.?3、知道观察到明显衍射的条件(二)能力目标了解单缝衍射、小孔衍射,并能用相关知识对生活中的有关现象进行解释和分析.(三)情感目标1、让学生知道科学研究必须重视理论的指导和实践的勤奋作用;2、必须有自信心和踏实勤奋的态度;3、在学习中也要有好品质、好作风.教学建议有关光的衍射的教学建议应该让学生了解,光的直进,是几何光学的基础,光的衍射现象并没有完全否定光的直进,而是指出了光的直进的适用
